设函数 $f(x)=x^2-a^x$（$a>0$ 且 $a\ne 1$），$g(x)=f'(x)$．
（1）当 $a={\rm e}$ 时，求 $g(x)$ 的极大值点；
（2）讨论 $f(x)$ 的零点个数．
已知 $\triangle ABC$ 的外心为 $O$，且满足 $\angle BAC=60^\circ$，$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$，且 $x\geqslant 0$，则 $x+4y$ 的最大值是_______．
设函数 $f(x)=(1-mx)\ln (1+x)$．
（1）当 $0<x<1$ 时，函数 $f(x)$ 的图象恒在 $y=x$ 上方，求实数 $m$ 的取值范围；
（2）求证：${\rm e}>\left(\dfrac{1001}{1000}\right)^{1000.4}$．
已知 $O$ 是 $\triangle ABC$ 外接圆的圆心，若 $A=\dfrac{\pi}3$，且 $\dfrac{\cos B}{\sin C}\overrightarrow {AB}+\dfrac{\cos C}{\sin B}\overrightarrow{AC}=2m\overrightarrow{AO}$，则 $m=$ ______．
已知 $f(x)=x\ln x+(1-x)\ln (1-x)$．
（1）求 $f(x)$ 的最小值；
（2）若 $a+b+c=1$，$a,b,c\in (0,1)$，求证：$a\ln a+b\ln b+c\ln c\geqslant (a-2)\ln 2$．
如图，已知矩形 $ABCD$ 中，$AB=x$，$BC=2$，$E,F$ 分别是线段 $AB,AD$ 的中点，$G,H$ 分别是线段 $CD,BC$ 上的动点（包括端点）．现将 $\triangle AEF$ 沿 $EF$ 翻折，使平面 $AEF\perp$ 平面 $BCDF$，同时将 $\triangle CGH$ 沿 $GH$ 翻折，若能使 $A,C$ 重合，则 $x$ 的最大取值为_______．
已知 $a,b$ 都是正数，$\triangle ABC$ 在平面直角坐标系 $xOy$ 内，以两点 $A(a,0)$ 和 $B(0,b)$ 为顶点的正三角形的第三个顶点 $C$ 在第一象限内．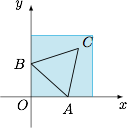
（1）若 $\triangle ABC$ 能包含于正方形 $D=\{(x,y)\mid 0\leqslant x\leqslant 1,0\leqslant y\leqslant 1\}$ 内，试求变量 $a,b$ 的约束条件，并在直角坐标系 $aOb$ 内画出这个约束条件表示的平面区域；
（2）当 $(a,b)$ 在第 $(1)$ 小题所得的约束条件内移动时，求 $\triangle ABC$ 面积的最大值，并求此时 $(a,b)$ 的值．
已知函数 $f(x)=x\ln x+x^2-ax+2$，其中 $a$ 是实数．若 $f(x)$ 有两个零点 $x_1,x_2$．
（1）求证：$x_1+x_2>2$；
（2）求证：$x_1\cdot x_2>1$．
已知 $I$ 是 $\triangle ABC$ 的内心，$AB=2$，$AC=3$，若 $\overrightarrow{AI}=x\overrightarrow{AB}+y\overrightarrow{AC}$，$2x+3y=m$，则 $m$ 的取值范围是________．
已知函数 $f(x)=\dfrac{2}{3}x^3+\dfrac 12ax^2+2bx+c$ 在区间 $(0,1)$ 上有极大值，在区间 $(1,2)$ 上有极小值，若 $(a+3)b\leqslant t$ 恒成立，则 $t$ 的取值范围是______．
