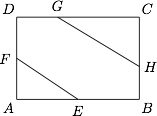
如图，已知矩形 $ABCD$ 中，$AB=x$，$BC=2$，$E,F$ 分别是线段 $AB,AD$ 的中点，$G,H$ 分别是线段 $CD,BC$ 上的动点（包括端点）．现将 $\triangle AEF$ 沿 $EF$ 翻折，使平面 $AEF\perp$ 平面 $BCDF$，同时将 $\triangle CGH$ 沿 $GH$ 翻折，若能使 $A,C$ 重合，则 $x$ 的最大取值为_______．
正确答案是$\sqrt{1+\sqrt{17}}$．
分析与解 显然 $x=2$ 符合题意，接下来考虑 $x>2$ 的情况．
如图，作 $AQ\perp EF$ 于 $Q$，连接 $CQ$，过 $Q$ 作 $CD$ 的垂线，垂足为 $P$，过 $B$ 作 $CQ$ 的垂线，垂足为 $K$．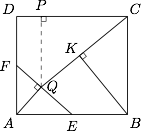
分析投影可知，若 $A,C$ 能够重合，必然有 $GH\perp CQ$，进而可得 $A,C$ 可以重合的充要条件是\[QA^2+QK^2\leqslant CK^2.\]以 $A$ 为坐标原点，$AB$ 为 $x$ 轴正方向建立平面直角坐标系，则\[AQ^2=\dfrac{1}{\dfrac{1}{AE^2}+\dfrac1{AF^2}}=\dfrac{x^2}{x^2+4},\]进而可得 $Q\left(\dfrac{2x}{x^2+4},\dfrac{x^2}{x^2+4}\right)$．记\[\angle QCP=\angle KBC=\theta,\]则\[\tan\theta=\dfrac{2-\dfrac{x^2}{x^2+4}}{x-\dfrac{2x}{x^2+4}}=\dfrac{x^2+8}{x^3+2x},\]因此\[QA^2+QK^2\leqslant CK^2\]即\[\begin{split} QA^2&\leqslant CK^2-QK^2\\&=(CK+QK)(CK-QK)\\&=2\cdot CQ\cdot CK-CQ^2\\&=2\cdot \dfrac{QP}{\sin\theta}\cdot BC\cdot \sin\theta-\dfrac{QP^2}{\sin^2\theta},\end{split}\]即\[\dfrac{x^2}{x^2+4}\leqslant 2\cdot \left(2-\dfrac{x^2}{x^2+4}\right)\cdot 2-\left(2-\dfrac{x^2}{x^2+4}\right)^2\cdot \left[1+\left(\dfrac{x^3+2x}{x^2+8}\right)^2\right],\]整理得\[x^4-2x^2-16\leqslant 0,\]解得\[2<x\leqslant\sqrt{1+\sqrt{17}},\]因此所求 $x$ 的最大值为 $\sqrt{1+\sqrt{17}}$．