已知 $a,b$ 都是正数，$\triangle ABC$ 在平面直角坐标系 $xOy$ 内，以两点 $A(a,0)$ 和 $B(0,b)$ 为顶点的正三角形的第三个顶点 $C$ 在第一象限内．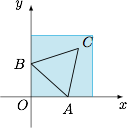
（1）若 $\triangle ABC$ 能包含于正方形 $D=\{(x,y)\mid 0\leqslant x\leqslant 1,0\leqslant y\leqslant 1\}$ 内，试求变量 $a,b$ 的约束条件，并在直角坐标系 $aOb$ 内画出这个约束条件表示的平面区域；
（2）当 $(a,b)$ 在第 $(1)$ 小题所得的约束条件内移动时，求 $\triangle ABC$ 面积的最大值，并求此时 $(a,b)$ 的值．
分析与解 （1）设 $C(x,y)$，则\[\begin{cases} (x-a)^2+y^2=a^2+b^2,\\ x^2+(y-b)^2=a^2+b^2,\end{cases}\]解得\[\left(x,y\right)=\left(\dfrac{a+\sqrt 3b}2,\dfrac{\sqrt 3a+b}2\right),\]因此变量 $a,b$ 的约束条件是\[\begin{cases} 0<a\leqslant 1,\\ 0<b\leqslant 1,\\ a+\sqrt 3b\leqslant 2,\\ \sqrt 3a+b\leqslant 2.\end{cases}\]在直角坐标系 $aOb$ 中的平面区域如图所示，为六边形 $OMTPSN$ 内部以及边界（不包含边 $OM,ON$）．
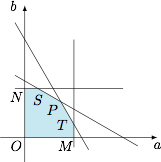其中 $M\left(1,0\right)$，$N\left(0,1\right)$，$P\left(\sqrt 3-1,\sqrt 3-1\right)$，$S\left(2-\sqrt 3,1\right)$，$ T\left(1,2-\sqrt3\right)$．
（2）考虑到\[\begin{split} &OM^2=ON^2=1,\\&OT^2=OS^2=OP^2=8-4\sqrt 3,\end{split}\]于是 $\triangle ABC$ 面积的最大值为\[\dfrac{\sqrt 3}4\cdot \left(8-4\sqrt 3\right)=2\sqrt 3-3,\]此时 $(a,b)=\left(1,2-\sqrt 3\right),\left(2-\sqrt 3,1\right),\left(\sqrt 3-1,\sqrt 3-1\right)$．