已知 $\triangle A B C$ 外接圆 $O$ 的半径为 $1$,$ \angle A$ 的角平分线交圆 $O$ 于另一点 $D$,$ A D=\sqrt{3}$,则 $\angle C A D$ 的取值范围是_____,$\overrightarrow{A B} \cdot \overrightarrow{A C}$ 的最小值是_____.
每日一题[4029]抽卡常识
一个游戏 $\rm UP$ 池中有 $n$ 张不同的角色卡,每次抽奖独立地从中抽取 $1$ 张(有放回的抽取),第一次获取角色卡后得到该角色,之后再获得该角色将得到星辉(可用于兑换抽卡资源,但不影响抽卡次数).
1、求经过 $k$ 抽后,获取的不同角色个数的数学期望;
2、求获取卡池中所有角色需要抽数的数学期望.
每日一题[4028]裂项与构造
已知 $n\in\mathbb N^{\ast}$,正实数 $a_1,a_2,\cdots,a_n$ 的前 $k$ 项和为 $S_k$ 且 $S_n=1$,求证:$\displaystyle 1\leqslant \sum\limits_{k=1}^n\dfrac{a_k}{\sqrt{S_k}}<2$.
每日一题[4027]论证与构造
已知椭圆 $\Gamma:\dfrac{y^2}{a^2}+\dfrac{x^2}{b^2}=1$($a>b>0$)的上顶点为 $S(0,\sqrt 6)$,且过点 $P(1,\sqrt 3)$.
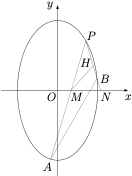
1、求椭圆 $\Gamma$ 的方程;
2、若斜率为 $\sqrt 3$ 的直线 $l$ 与椭圆交于 $A, B$ 两点(直线 $PA$ 斜率为正),直线 $PA, PB$(若 $P,B$ 重合,直线 $PB$ 即为椭圆 $\Gamma$ 在 $P$ 点处的切线)分别与 $x$ 轴交于 $M, N$ 两点,$H$ 为 $PN$ 中点.
① 求 $\sin\angle PMH$ 的最大值;
② 当 $\sin\angle PMH$ 最大时,将坐标平面沿 $x$ 轴折成二面角 $P-MN-A$,在二面角 $P-MN-A$ 大小变化过程中,求三棱锥 $P-MNA$ 外接球表面积取得最小值时三棱锥 $P-MNA$ 的内切球的半径.
每日一题[4026]可行域
已知实数 $x,y$ 满足:$2\leqslant x+y\leqslant 3$,$1\leqslant x+y^2\leqslant 4$,则 ( )
A.$x$ 的最小值为 $0$
B.$y$ 的的最大值为 $2$
C.$(x+y)(x^2+y^2)$ 的最小值为 $2$
D.$(x+y)(x^2+y^2)$ 的最大值为 $12$
每日一题[4025]迭代向前
已知增函数 $f(x)$ 满足当 $x\in \mathbb N^{\ast}$ 时,$f(x)\in\mathbb N^{\ast}$,且 $f(f(n))=2n+1$,则( )
A.$f(1)=2$
B.$f(4)=6$
C.$f(2025)=2536$
D.$f(2^n)=3\cdot 2^{n-1}$($n\in\mathbb N^{\ast}$)
每日一题[4024]椭圆的光学性质
己知椭圆 $C: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 $($a>b>0$)的左,右焦点分别为 $F_1, F_2$,点 $A$ 是 $C$ 上的一点($A$ 在第一象限)且 $\angle F_1 A F_2=90^{\circ}$,$\angle F_1 A F_2$ 的角平分线 $l$ 与 $C$ 的另一个交点为点 $B$,$l$ 与 $y$ 轴交于点 $D$,若 $|A B|=2 |B D|$,则 $C$ 的离心率为_____.
每日一题[4023]函数与方程
在 $\triangle A B C$ 中,$\sin ^2 A+\sin ^2 B=\sin (A+B)$ 是 $C$ 为直角的( )
A.充分但非必要条件
B.必要但非充分条件
C.充要条件
D.既非充分条件也非必要条件
每日一题[4022]代数变形
已知实数 $a, b$ 满足 $3^a+5^b=9^a+25^b$,则 $27^a+125^b$ 的最大值为_____.
每日一题[4021]函数最值与消元
2026年1月湖南雅礼中学高三期末数学考试 #11
已知 $g(x)=2+m\cos x+n\sin x+M\cos 2 x+N\sin 2 x$,其中 $m,n,M,N$ 为常数, 且 $g(x)\geqslant 0$ 对任意 $x\in\mathbb R$ 恒成立,则( )
A.$m^2+n^2\leqslant 8$
B.$M^2+N^2>4$
C.$|m|+|n|+|M|+|N|\leqslant 2\sqrt 2+4$
D.$g(x)\leqslant 6$
