以下是面点师一个工作环节的数学模型：如图，在数轴上截取与闭区间$[0,4]$对应的线段，对折后（坐标$4$对应的点与原点重合）再均匀地拉成$4$个单位长度的线段，这一过程称为一次操作（例如在第一次操作完成后，原来的坐标$1$、$3$变成$2$，原来的坐标$2$变成$4$，等等）．
那么原闭区间$[0,4]$上（除两个端点外）的点，在第$n$次操作完成后（$n\geqslant 1$），恰好被拉到与$4$重合的点所对应的坐标为$f(n)$，则$f(3)=$_____，$f(n)=$_____．
设$O$为$\triangle ABC$的外心，$x \overrightarrow {OA}+y\overrightarrow {OB}+z\overrightarrow {OC}=\overrightarrow {0}$，$xyz\ne 0$，$C$为$\triangle ABC$的内角，则$\cos{2C}=$_____．（用$x,y,z$表示）
已知有公共焦点的椭圆与双曲线中心为原点，焦点在$x$轴上，左右焦点分别为$F_1,F_2$，且它们在第一象限的交点为$P$，$\triangle PF_1F_2$是以$PF_1$为底边的等腰三角形，若双曲线的离心率的取值范围为$(1,2)$，则该椭圆的离心率的取值范围是_____．
在正方形\(ABCD\)的外侧作直线\(AP\)，点\(B\)关于直线\(AP\)的对称点为\(E\)，连接\(BE，DE\)，其中\(DE\)交直线\(AP\)于点\(F\)．若\(45^\circ<\angle PAB<90^\circ\)，则\(AB，EF，FD\)存在怎样的等量关系？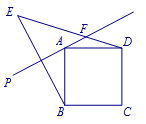
继续阅读
已知$f(x)$的定义域为$\mathcal{R}$，$f(1)=\dfrac 14$，且满足$$4f(x)f(y)=f(x+y)+f(x-y),$$则$f(2016)=$_____．
已知函数$f(x)=ax^2+bx+c$，且$a>b>c$，$a+b+c=0$，集合$A=\{m|f(m)<0\}$，则（ ）
A．$\forall m\in A$，都有$f(m+3)>0$
B．$\forall m\in A$，都有$f(m+3)<0$
C．$\exists m_0\in A$，使得$f(m_0+3)=0$
D．$\exists m_0\in A$，使得$f(m_0+3)<0$
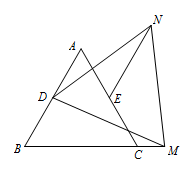
如图，在等边\(\triangle ABC\)中，\(D,E\)分别为\(AB,AC\)的中点，\(M\)为射线\(BC\)上一动点，在\(B\)点异侧作等边\(\triangle DMN\)，判断\(EN\)与\(AB\)的位置关系，并给出证明．
继续阅读
2012年高考数学江苏卷第14题（填空压轴题）：
已知正数$a,b,c$满足：$5c-3a\leqslant b\leqslant 4c-a$，$c\ln b\geqslant a+c\ln c$，则$\dfrac ba$的取值范围是_____．
2015年已接近尾声，2016年即将来到．据说在近期北理工的数学分析课上，老师给同学们的祝福语相当别致：
设$a_1=\sqrt{1+2015}$，$a_2=\sqrt{1+2015\sqrt{1+2016}}$，$a_3=\sqrt{1+2015\sqrt{1+2016\sqrt{1+2017}}}$，
一般的，设$a_n=\sqrt{1+2015\sqrt{1+2016\sqrt{1+\cdots+(2013+n)\sqrt{1+(2014+n)}}}}$，$n\in \mathbf {N_+}$．
求证：数列$\{a_n\}$收敛，并求$\lim\limits_{n \to \infty}a_n$的值．
谨以此题恭贺2016年新年！
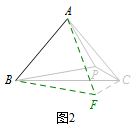
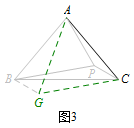
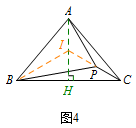
等腰三角形内一点与三顶点连线组成的图形问题，通常以等腰三角形的一条边向同侧作等边三角形，从而得到更多的边等角等（如图1~3）；当然有时也能由等腰三角形的对称性来解决问题（如图4）．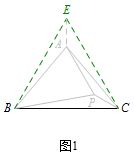
继续阅读
