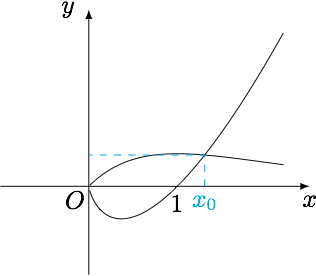
解析几何中有一类问题是:求点$M(a,b)$关于直线$l:Ax+By+C=0$的对称点$N$.这类问题的常规思路是:通过$MN\perp l$且$MN$的中点在直线$l$上两个条件求解,计算量较大.当直线$l$的斜率为$\pm 1$时,坐标可以直接心算得到,结论如下: 继续阅读
2025年 12月 一 二 三 四 五 六 日 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 标签
-
近期文章
2025年 12月 一 二 三 四 五 六 日 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 标签