设数列$a_1,a_2,a_3,\cdots ,a_{21}$满足:$\left|a_{n+1}-a_n\right|=1$($n=1,2,3,\cdots,20$),$a_1,a_7,a_{21}$成等比数列.若$a_1=1$,$a_{21}=9$,则满足条件的不同数列的个数为_______.
每日一题[952]相对运动
棱长为$2$的正方体$ABCD-A_1B_1C_1D_1$在空间直角坐标系$O-xyz$中运动,其中顶点$A$保持在$z$轴上,顶点$B_1$保持在平面$xOy$上,则$OC$长度的最小值是_____.
每日一题[951]图形对称
已知$x_1,x_2$分别是关于$x$的方程$x{\rm e}^x={\rm e}^2$和$x\ln x={\rm e}^2$的解,则$x_1x_2$的值是________.
每日一题[950]二元不等式的恒成立
已知实数$a,b>0$,$f(x)=ax^2+b$满足对于任意$x,y\in\mathbb R$,$$f(xy)+f(x+y)\geqslant f(x)\cdot f(y),$$求实数$a,b$需要满足的条件.
每日一题[949]转化为距离
已知$O$是$\triangle ABC$的外心,$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$,若$A$是锐角且满足\[3\sqrt{41-40\cos A}+4\sqrt{34-30\sin A}=25,\]则$x+y$的最大值为_______.
每日一题[948]简洁明了
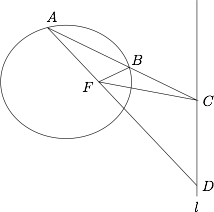
如图,已知椭圆$\Gamma$的一个焦点为$F$,与其对应的准线为$l$.直线$AB$交椭圆$\Gamma$于$A,B$两点,交准线$l$于点$C$.直线$AF$交准线$l$于点$D$.求证:$FC$平分$\angle BFD$.
 继续阅读
继续阅读
每日一题[947]兵分三路证对称
已知椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (a>b>0)$的短轴长为$2\sqrt{3}$,右焦点为$F(1,0)$,
点$M$是椭圆$C$上异于左、右顶点$A,B$的一点.
(1) 求椭圆$C$的方程;
(2) 若直线$AM$与直线$x=2$交于点$N$,线段$BN$的中点为$E$.证明:点$B$关于直线$EF$的对称点在直线$MF$上.
每日一题[946]新定义关系
据统计某超市两种蔬菜$A,B$连续$n$天价格分别为$a_1,a_2,\cdots,a_n$和$b_1,b_2,\cdots,b_n$,令$$M=\left\{m\left|\ a_m<b_m,\ m=1,2,\cdots,n\right.\right\},$$若$M$中元素个数大于$\dfrac{3}{4}n$,则称蔬菜$A$在这$n$天的价格低于蔬菜$B$的价格,记作$A\prec B$.现有三种蔬菜$A,B,C$,下列说法正确的是( )
A.若$A\prec B,B\prec C$,则$A\prec C$
B.若$A\prec B,B\prec C$同时不成立,则$A\prec C$不成立
C.$A\prec B,B\prec A$可同时不成立
D.$A\prec B,B\prec A$可同时成立
每日一题[945]构造与论证
各项均为非负整数的数列$\left\{a_n\right\}$同时满足下列条件:
①$a_1=m$,其中$m\in \mathbb{N}^{*}$;
②当正整数$n \geqslant 2$时,恒有$a_n \leqslant n-1$;
③对任意正整数$n$,均有$n$是$S_n=a_1+a_2+\cdots+a_n$的因数.
(1) 当$m=5$时,写出数列$\left\{a_n\right\}$的前五项;
(2) 若数列$\left\{a_n\right\}$的前三项互不相等,且正整数$n \geqslant 3$时,$a_n$为常数,求$m$的值;
(3) 求证:对任意正整数$m$,都存在正整数$M$,只要正整数$n \geqslant M$,均有$a_n$为常数.
每日一题[944]必要条件探路
已知函数$f(x)=\mathrm{e}^x+x^2-x$,$g(x)=x^2+ax+b$,其中$a,b$均为实数.
(1) 当$a=1$时,求函数$F(x)=f(x)-g(x)$的单调区间;
(2) 若曲线$y=f(x)$在点$(0,1)$处的切线$l$与曲线$y=g(x)$切于点$(1,c)$,求$a,b,c$的值;
(3) 若$f(x)\geqslant g(x)$恒成立,求$a+b$的最大值.
