已知椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (a>b>0)$的短轴长为$2\sqrt{3}$，右焦点为$F(1,0)$，
点$M$是椭圆$C$上异于左、右顶点$A,B$的一点．
(1) 求椭圆$C$的方程；
(2) 若直线$AM$与直线$x=2$交于点$N$，线段$BN$的中点为$E$．证明：点$B$关于直线$EF$的对称点在直线$MF$上．
分析与解 (1) $\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$．
(2)方法一 如图，作椭圆$C$的右准线$x=4$，作$MH$垂直右准线$x=4$于点$H$．
设直线$AM$交右准线$x=4$于点$G$，设直线$FG$交直线$x=2$于点$E_1$，因为\[\dfrac{|FA|}{|FM|}=\dfrac{|DA|}{|HM|}=\dfrac{|GA|}{|GM|},\]所以$FG$是$\triangle FAM$中$\angle AFM$的外角平分线，即$FG$平分$\angle BFM$．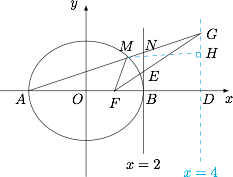
注意到\[\dfrac{\left|E_1B\right|}{|GD|}=\dfrac{1}{3},\ \dfrac{\left|NB\right|}{|GD|}=\dfrac{2}{3},\]故点$E_1$与点$E$重合，所以$FE$平分$\angle BFM$，进而点$B$关于直线$EF$的对称点在直线$MF$上．
方法二 根据椭圆的垂径定理的推论，可设\[AM:x=\dfrac 1ky-2,BM:x=-\dfrac{4k}3y+2,\]于是可得\[M\left(\dfrac{6-8k^2}{3+4k^2},\dfrac{12k}{3+4k^2}\right),\]因此直线$MF$的斜率为\[\dfrac{\dfrac{12k}{3+4k^2}}{\dfrac{6-8k^2}{3+4k^2}-1}=\dfrac{4k}{1-4k^2}=\dfrac {2\cdot(2k)}{1-(2k)^2},\]而直线$EF$的斜率为$2k$，因此命题得证．
方法三 利用仿射变换不难证明直线$ME$与椭圆相切．设直线$ME$与$x$相交于点$T$，利用椭圆的极点极线性质可得$M$点的横坐标$x_M$与$T$点的横坐标$x_T$满足\[x_M\cdot x_T=4,\]而\[\begin{split}\angle MFE=\angle BFE &\Leftarrow \dfrac{ME}{ET}=\dfrac{FM}{FT}\\&\Leftarrow \dfrac{2-x_M}{x_T-2}=\dfrac{2-\dfrac 12x_M}{x_T-1}\\&\Leftarrow x_M\cdot x_T=4,\end{split}\]因此原命题得证．