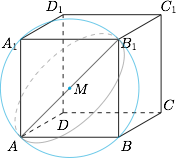
棱长为$2$的正方体$ABCD-A_1B_1C_1D_1$在空间直角坐标系$O-xyz$中运动，其中顶点$A$保持在$z$轴上，顶点$B_1$保持在平面$xOy$上，则$OC$长度的最小值是_____．
正确答案是$\sqrt 6-\sqrt 2$．
分析与解 考虑让正方体$ABCD-A_1B_1C_1D_1$静止，坐标系运动．由于$OA\perp OB_1$，于是$O$点在以$AB_1$为直径的球面上运动．设该球面的球心为$M$，则其半径$$r=MA=\dfrac 12AB_1=\sqrt 2,$$而$MC=\sqrt 6$，因此$OC$长度的最小值为\[|MC-r|=\sqrt 6-\sqrt 2.\]