设$\triangle ABC$的周长为$12$，内切圆的半径为$1$，则（ ）
A．$\triangle ABC$必为直角三角形
B．$\triangle ABC$必为锐角三角形
C．$\triangle ABC$必为直角三角形或锐角三角形
D．以上结论都不对
已知 $g(x)=x^2-2ax+1$ 在区间 $[1,3]$ 上的值域为 $[0,4]$．
（1）求 $a$ 的值；
（2）若不等式 $g\left(2^x\right)-k\cdot 4^x\geqslant 0$ 在 $x\in [1,+\infty)$ 上恒成立，求实数 $k$ 的取值范围；
（3）若函数 $$y=\dfrac{g\left(|2^x-1|\right)}{|2^x-1|}+k\cdot \dfrac{2}{|2^x-1|}-3k$$ 有 $3$ 个零点，求实数 $k$ 的取值范围．
已知函数 $f(x)$ 的定义域为 $(0,+\infty)$，若 $y=\dfrac{f(x)}{x^k}$ 在 $(0,+\infty)$ 上为增函数，其中 $k$ 为正整数，则称 $f(x)$ 为 $k$ 阶比增函数．
（1）已知函数 $f(x)=x^3-2hx^2-hx$，若 $f(x)$ 是 $1$ 阶比增函数，但不是 $2$ 阶比增函数，求实数 $h$ 的取值范围；
（2）已知实数 $m$ 满足对 任意 $2$ 阶比增函数 $f(x)$，均有 $f(x)<m$，求 $m$ 的最小值．
已知函数 $f(x)=\ln (1+x)-x$．
（1）求 $f(x)$ 的单调区间；
（2）记 $f(x)$ 在区间 $[0,n]$（$n\in\mathbb N^{\ast}$）上的最小值为 $b_n$，令 $a_n=\ln(1+n)-b_n$．若对任意正整数 $n$，不等式 $\sqrt{a_n}<\sqrt{a_{n+2}}-\dfrac c{\sqrt{a_{n+2}}}$ 恒成立，求实数 $c$ 的取值范围；
（3）在第 $(2)$ 小题的条件下，求证：$$ \dfrac{a_1}{a_2}+\dfrac{a_1a_3}{a_2a_4}+\cdots+\dfrac{a_1a_3\cdots a_{2n-1}}{a_2a_4\cdots a_{2n}}<\sqrt{2a_n+1}-1.$$
在 $\triangle ABC$ 中，三个内角满足关系式 $y=2+\cos C\cdot \cos (A-B)-\cos^2C$．
（1）若任意交换两个角的位置，$y$ 的值是否会发生变化，并证明你的结论；
（2）求 $y$ 的最大值．
关于 $x$ 的不等式 $(ax-1)(\ln x+ax)\geqslant 0$ 在 $(0,+\infty)$ 上恒成立，则实数 $a$ 的取值范围是_______．
如图，在边长为 $\sqrt 3$ 的菱形 $ABCD$ 中，$\angle DAB=\dfrac{\pi}3$，$DE=\dfrac 12EC$，$F$ 为线段 $BC$ 的中点，$G$ 为 $EF$ 上的一点，且 $\overrightarrow{AG}=\dfrac 12\overrightarrow{AC}+t\overrightarrow{AD}$，则 $\left|\overrightarrow{BG}\right|$ 的值是（ ）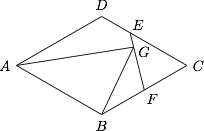
A．$\dfrac{\sqrt{111}}8$
B．$\dfrac{3\sqrt{17}}8$
C．$\dfrac{\sqrt{79}}8$
D．$\dfrac{\sqrt {66}}8$
已知实数 $x,y$ 满足 $x^2+y^2-10x-10y+45=0$，则 $\dfrac{2x^2-xy-y}{x}$ 的最小值是_______．
已知函数 $f(x)=\ln\left(\dfrac 12+\dfrac 12ax\right)+x^2-ax$（$a$ 为常数，$a>0$）．
（1）当 $a=1$ 时，求函数 $f(x)$ 在 $x=1$ 处的切线方程；
（2）当 $y=f(x)$ 在 $x=\dfrac 12$ 处取得极值时，若关于 $x$ 的方程 $f(x)-b=0$ 在 $[0,2]$ 上恰有 $2$ 个实数解，求实数 $b$ 的取值范围；
（3）若对任意的 $a\in(1,2)$，总存在 $x_0\in\left[\dfrac 12,1\right]$，使不等式 $f(x_0)>m\left(a^2+2a-3\right)$ 成立，求实数 $m$ 的取值范围．
已知椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的左、右顶点分别为 $A_1,A_2$，上、下顶点分别为 $B_2,B_1$，左、右焦点分别为 $F_1,F_2$，其中长轴长为 $4$，且圆 $O:x^2+y^2=\dfrac{12}7$ 为菱形 $A_1B_1A_2B_2$ 的内切圆．
（1）求椭圆 $C$ 的方程；
（2）点 $N(n,0)$ 为 $x$ 轴正半轴上一点，过点 $N$ 作椭圆 $C$ 的切线 $l$，记右焦点 $F_2$ 在 $l$ 上的射影为 $H$，若 $\triangle F_1HN$ 的面积不小于 $\dfrac{3}{16}n^2$，求 $n$ 的取值范围．
