设函数$f(x)={\rm e}^x-x$，$g(x)=-kx^3+kx^2-x+1$．
(1)求$f(x)$的最小值；
(2)若使得对任意$x\in [0,1]$均有$f(x)\geqslant g(x)$成立的$k$的最大值为$\lambda$，求证：$5<\lambda<5.2$．
每日一题[979]放缩与估计
练习题集[96]基础练习
1．有$A,B,C$三种粒子，其中$A$有$20$个，$B$有$18$个，$C$有$16$个．已知其中任何两种不同的粒子各$1$个可以经过操作得到$2$个第三种粒子，问是否存在使得这三种粒子变成同一种粒子的操作方案．
2．设抛物线$C:y^2=2px$($p>0$)的焦点为$F$，点$M$在$C$上，$|MF|=5$．若以$MF$为直径的圆过点$(0,2)$，则$C$的方程为( )
A．$y^2=4x$或$y^2=8x$
B．$y^2=2x$或$y^2=8x$
C．$y^2=4x$或$y^2=16x$
D．$y^2=2x$或$y^2=16x$
3．已知$x>0$，求$y=\sqrt{\dfrac{1}{1+x^2}}+2\sqrt{\dfrac{x}{1+x}}$的最大值．
4．设$F$为抛物线$y^2=4x$的焦点，$A,B,C$为该抛物线上三点，若$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$，则$|\overrightarrow{FA}|+|\overrightarrow{FB}|+|\overrightarrow{FC}|=$______．
5．已知数列$\{a_n\}$满足条件$a_{n+1}=-\dfrac{(a_n+1)^2}{a_n+2}$，首项$a_1=-\dfrac 12$，求$\lim\limits_{n\to \infty}a_n$．
6．使得$2016+2^n$为完全平方数的正整数$n$的个数为( )
A．$0$
B．$1$
C．$2$
D．无穷个
7．设$x=1+\sqrt 2+\sqrt 3$为整系数多项式$p(x)=x^4+ax^3+bx^2+cx+d$的一个根，则$d$的值是_______．
参考答案
1．可能的操作如下表．\[\begin{matrix} A&B&C\\ +2& -1&-1\\ -1&+2&-1\\ -1&-1&+2\\ \end{matrix}\]根据题意，无论如何操作，粒子$A$与$B$的个数之差的变换量一定为$3$的倍数，因此粒子$A$与$B$的数量之差必然模$3$余$2$，不可能存在使得这三种粒子变成同一种粒子的操作方案．
注 粒子$A$与$B$的数量之差模$3$的余数是操作下的不变量．
2．C．
一方面，根据抛物线的定义易得以$MF$为直径的圆与$y$轴相切，结合题意可得切点为$(0,2)$，于是线段$MF$的中点纵坐标为$2$，进而$M$点的纵坐标为$4$，于是$M\left(\dfrac{8}{p},4\right)$．另一方面，由$MF=5$，可得$M$点的横坐标为$5-\dfrac p2$．因此\[\dfrac 8p=5-\dfrac p2,\]解得$p=2$或$p=8$．
3．$\dfrac{3\sqrt 2}2$．
令$x=\tan \theta$，$\theta\in\left(0,\dfrac{\pi}2\right)$，则\[y=\cos \theta+2\sqrt{\dfrac{\sin \theta}{\sin \theta+\cos \theta}},\]其导函数\[y'_{\theta}=\sqrt{\dfrac{1}{\sin\theta\left(\sin\theta+\cos\theta\right)^3}}-\sin \theta=\sqrt{\dfrac{1}{\left(\sin ^2\theta+\sin\theta\cos\theta\right)^3}\cdot \sin^2\theta}-\sqrt{\sin^2\theta},\]而\[\sin^2\theta+\sin\theta\cos\theta=\dfrac {1+\sqrt 2\sin\left(2\theta-\dfrac{\pi}4\right)}2,\]于是当$\theta\in\left(0,\dfrac{\pi}4\right)$时，$y_{\theta}$单调递增；当$\theta\in\left(\dfrac{\pi}4,\dfrac{\pi}2\right)$时，$y_{\theta}$单调递减；当$\theta=\dfrac{\pi}4$时，$y_{\theta}$取得最大值$\dfrac{3\sqrt 2}2$．因此所求的最大值为$\dfrac{3\sqrt 2}2$．
4．$6$．
设$A,B,C$的横坐标分别为$x_1,x_2,x_3$，根据题意，有\[x_1+x_2+x_3=3\cdot \dfrac p2=3,\]其中$\dfrac p2$为$F$的横坐标，于是\[|\overrightarrow{FA}|+|\overrightarrow{FB}|+|\overrightarrow{FC}|=(x_1+1)+(x_2+1)+(x_3+1)=(x_1+x_2+x_3)+3=6.\]
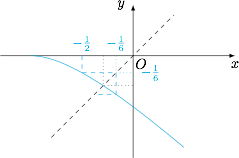
5．递推公式对应的不动点为$x=-1\pm\dfrac{\sqrt 2}2$，于是有\[\begin{aligned} a_{n+1}+1-\dfrac{\sqrt 2}2&=-\dfrac{\left(a_n+1-\dfrac{\sqrt 2}2\right)\left(a_n+\sqrt 2\right)}{a_n+2},\\ a_{n+1}+1+\dfrac{\sqrt 2}2&=-\dfrac{\left(a_n+1+\dfrac{\sqrt 2}2\right)\left(a_n-\sqrt 2\right)}{a_n+2},\end{aligned}\]迭代函数$$f(x)=-\dfrac {(x+1)^2}{x+2}=-\left[(x+2)+\dfrac 1{x+2}\right]+2,$$在$(-1,+\infty)$上单调递减，容易证明\[-\dfrac 12\leqslant a_n\leqslant -\dfrac 16,\]
于是\[\left|-\dfrac{a_n+\sqrt 2}{a_n+2}\right|<\dfrac{2\sqrt 2-1}3<1,\]因此\[\lim\limits_{n\to \infty}a_n=-1+\dfrac{\sqrt 2}2.\]6．A．
考虑到$2016=2^5\cdot 63$，而当$n=1,2,3,4,5$时，$2016+2^n$不是完全平方数，于是$n\geqslant 6$，此时\[126+2^{n-4}\equiv 2\pmod 4,\]于是$126+2^{n-4}$不是完全平方数．因此不存在使得$2016+2^n$为完全平方数的正整数$n$．
7．$-8$．
根据题意，该整系数多项式的四个根分别为\[1+\sqrt 2+\sqrt 3,1+\sqrt 2-\sqrt 3,1-\sqrt 2+\sqrt 3,1-\sqrt 2-\sqrt 3,\]因此\[d=\left[(1+\sqrt 2)^2-3\right]\cdot \left[(1-\sqrt 2)^2-3\right]=-8.\]事实上，有\[p(x)=x^4-4x^3-4x^2+16x-8.\]
每日一题[977]翻杯子
对于$n$维向量$A=\left(a_1,a_2,\cdots,a_n\right)$，若对任意$i\in\{1,2,\cdots,n\}$均有$a_i=0$或$a_i=1$，则称$A$为$n$维$T$向量．对于两个$n$维$T$向量$A,B$，定义$d(A,B)=\displaystyle\sum_{i=1}^{n}\left|a_i-b_i\right|$．
(1) 若$A=(1,0,1,0,1)$，$B=(0,1,1,1,0)$，求$d(A,B)$的值；
(2) 现有一个$5$维$T$向量序列：$A_1,A_2,A_3,\cdots$，若$A_1=(1,1,1,1,1)$，且对任意正整数$i$，均有$d\left(A_i,A_{i+1}\right)=2$，求证：该序列中不存在$5$维$T$向量序列$(0,0,0,0,0)$；
(3) 现有一个$12$维$T$向量序列：$A_1,A_2,A_3,\cdots$，若$A_1=(\underbrace{1,1,\cdots,1}_{12\,\text{个}})$，$A_j=(\underbrace{0,0,\cdots,0}_{12\,\text{个}})$，$j\in \mathbb{N}^{*}$，且存在正整数$m$，使得对任意正整数$i$，均有$d\left(A_i,A_{i+1}\right)=m$，求出所有可能的$m$．
继续阅读
数列的构造与论证
一列正整数$a_1,a_2,\cdots,a_n,\cdots$满足每个数都能整除之后的数，即$a_n\mid a_{n+1}$，则它们模$30$的余数最多可能有多少种不同的取值？
每日一题[976]各有千秋
已知$a,b\in \left[1,\sqrt 3\right]$，则$\dfrac{a^2+b^2-1}{ab}$的取值范围是______．
继续阅读
每日一题[975]限制条件下的最值
在$\triangle ABC$中，角$A,B,C$所对的边分别为$a,b,c$，且$\left|\overrightarrow{BA}+\overrightarrow{BC}\right|=2$，$\overrightarrow{AB}\cdot \overrightarrow{AC}=2$，则$b^2-ab$的最小值为_______．
继续阅读
每日一题[974]数列的新定义问题
对于无穷数列$\left\{a_n\right\}$，记$T=\left\{x\left|\ x=a_j-a_i,\ i<j\right.\right\}$，若数列$\left\{a_n\right\}$满足：存在$t\in T$，使得只要$a_m-a_k=t$（$m,k\in \mathbb{N}^{*}$且$m>k$），必有$a_{m+1}-a_{k+1}=t$，则称数列$\left\{a_n\right\}$具有性质$P(t)$．
(1) 若数列$\left\{a_n\right\}$满足\[a_n=\begin{cases}2n,&n \leqslant 2,\\2n-5,&n \geqslant 3,\end{cases}\]判断数列$\left\{a_n\right\}$是否具有性质$P(2)$？是否具有性质$P(4)$？（只需写出判断结果）
(2) 求证：$T$是有限集是数列$\left\{a_n\right\}$具有性质$P(0)$的必要不充分条件；
(3) 已知$\left\{a_n\right\}$是各项均为正整数的数列，且$\left\{a_n\right\}$既具有性质$P(2)$，又具有性质$P(5)$，求证：存在整数$N$，使得$a_N,a_{N+1},a_{N+2},\cdots$是等差数列．
每日一题[973]必要条件探路
设$a<0$，且$\forall x\in (a,b),\left(x^2+2017a\right)(x+2016b)\geqslant 0$，则$b-a$的最大值为_______．
继续阅读
每日一题[972]极值的存在性
已知函数$f(x)=(x-a)^2\ln x$，$a\in\mathbb R$．
(1) 若$a=3\sqrt{\rm e}$，求函数$g(x)=\dfrac{f(x)}{x}$的单调区间；
(2) 若函数$f(x)$既有极大值，又有极小值，求实数$a$的取值范围．
继续阅读