证明级数不等式的积分放缩法

我们先来看一下2003年高考江苏卷的压轴题：

例题1     （2003年江苏）设$a > 0$，如图．已知直线：$y = ax$及曲线$C$：$y = {x^2}$，$C$上的点${Q_1}$的横坐标为${a_1}$（$0 < {a_1} < a$）．从$C$上的点${Q_n}$（$n \geqslant 1$）作直线平行于$x$轴，交直线$l$于点${P_{n + 1}}$，再从${P_{n + 1}}$作直线平行于$y$轴，交曲线$C$于点${Q_{n + 1}}$．${Q_n}$（$n = 1 , 2 , \cdots$）的横坐标构成数列$\left\{ {{a_n}} \right\}$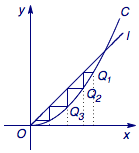．（1）试求${a_{n + 1}}$与${a_n}$的关系，并求$\left\{ {{a_n}} \right\}$的通项公式．

（2）当$a = 1$，${a_1} \leqslant \dfrac{1}{2}$时，证明：$\sum\limits_{k = 1}^n {\left( {{a_k}-{a_{k + 1}}} \right){a_{k + 2}}} < \dfrac{1}{{32}}$；

（3）当$a = 1$时，证明：$\sum\limits_{i = 1}^n {\left( {{a_i}-{a_{i + 1}}} \right){a_{i + 2}}} < \dfrac{1}{3}$．

（1）解    容易得到

$$a_{n+1}=\dfrac{a_n^2}{a},$$ 于是不难求出$\{a_n\}$的通项为 $$a_n=a\cdot\left(\dfrac{a_1}a\right)^{2^{n-1}},n\in \mathcal N^*.$$

（2）证明    注意到$\{a_n\}$单调递减且有界，考虑直接通过有界性放缩：

$$\begin{split} \sum\limits_{k=1}^n\left(a_k-a_{k+1}\right)a_{k+2}&\leqslant \dfrac{1}{16}\sum_{k=1}^n\left(a_k-a_{k+1}\right)\\&=\dfrac 1{16}\left(a_1-a_{n+1}\right)\\&<\dfrac 1{32}.\end{split}$$

（3）证明    此时由于数列的上界为$1$，因此如果按解决第（2）小题的方式无法得到$\dfrac 13$这样的结果．

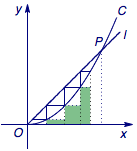
如图，注意到第$k$个小矩形（从右向左）的面积为

$$\left( {{a_k}-{a_{k + 1}}} \right) \cdot a_{k + 1}^2 = \left( {{a_k}-{a_{k + 1}}} \right) \cdot {a_{k + 2}},$$ 于是这些小矩形的面积和小于曲边三角形$OAP$的面积，其中$OP$为抛物线的一部分，$OA$、$AP$为线段，即 $$\sum\limits_{i = 1}^n {\left( {{a_i}-{a_{i + 1}}} \right){a_{i + 2}}} < \int_0^1 {{x^2}{\rm d}x} = \dfrac{1}{3}.$$

事实上，命题完全可以加强至

$$\sum\limits_{i = 0}^n {\left( {{a_i}-{a_{i + 1}}} \right){a_{i + 2}}} < \dfrac{1}{3},$$ 其中${a_0} = 1$．

---

从中我们可以看到利用函数定积分可以对数列级数进行有效的放缩．一般地，对于函数$f\left( x \right)$，$p$、$q$为整数且$p < q$，有以下引理：

引理    若$f\left( x \right)$单调递增，则

$$\int_{p - 1}^q {f\left( x \right){\rm d}x} < \sum\limits_{i = p}^q {f\left( i \right)} < \int_p^{q + 1} {f\left( x \right){\rm d}x} ;$$ 若$f\left( x \right)$单调递减，则 $$\int_p^{q + 1} {f\left( x \right){\rm d}x} < \sum\limits_{i = p}^q {f\left( i \right)} < \int_{p - 1}^q {f\left( x \right){\rm d}x}.$$

下面再通过一道联赛二试题看看这一处理方式的应用：

例题2   （2009年联赛加试）证明：$- 1 < \sum\limits_{i = 1}^n {\dfrac{i}{{{i^2} + 1}}} - \ln n \leqslant \dfrac{1}{2}$．

解    原不等式等价于

$$- 2 + \ln {n^2} < \sum\limits_{i = 1}^n {\dfrac{{2i}}{{{i^2} + 1}}} \leqslant 1 + \ln {n^2},$$ 对于函数$f\left( x \right) = \dfrac{{2x}}{{{x^2} + 1}}$，由于 $$f'\left( x \right) = \dfrac{{2\left( {1-{x^2}} \right)}}{{{{\left( {{x^2} + 1} \right)}^2}}},$$ 于是当$x \geqslant 1$时，$f\left( x \right)$单调递减．

由引理，有

$$\begin{split} \sum\limits_{i = 1}^n {\dfrac{{2i}}{{{i^2} + 1}}} &> \int_1^{n + 1} {\dfrac{{2x}}{{{x^2} + 1}}{\rm d}x} \\&= \left. {\ln \left( {{x^2} + 1} \right)} \right|_1^{n + 1}\\& = \ln{\dfrac{{{n^2} + 2n + 2}}{2}}\\&> \ln  {\dfrac{{{n^2}}}{{{{\text{e}}^2}}}} =-2 + \ln {n^2}.\end{split}$$

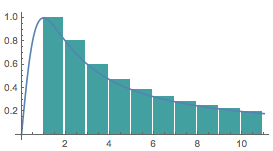
同时，有

$$\begin{split} \sum\limits_{i = 1}^n {\dfrac{{2i}}{{{i^2} + 1}}} &= 1 + \sum\limits_{i = 2}^n {\dfrac{{2i}}{{{i^2} + 1}}}\\& \leqslant 1 + \int_1^n {\dfrac{{2x}}{{{x^2} + 1}}{\rm d}x} \\&= 1 + \left. {\ln \left( {{x^2} + 1} \right)} \right|_1^n \\&= 1 + \ln  {\dfrac{{{n^2} + 1}}{2}} \leqslant 1 + \ln {n^2},\end{split}$$ 如图．

因此原命题得证．

---

在实际应用中，为了实现更精确的放缩，我们有两种处理方式：移动放缩起点和进一步利用凹凸性精细化放缩．下面通过一道例题说明这两种不同的方式．

例题3     （2013年深圳一模）证明：$\sum\limits_{k = 1}^n {\dfrac{{4k}}{{4{k^2} -1}}} > \ln \left( {2n + 1} \right)$．

解    后移起点

不等式左边即

$$\begin{split} \sum\limits_{k = 1}^n {\dfrac{{4k}}{{4{k^2}-1}}} &= \sum\limits_{k = 1}^n {\left( {\dfrac{1}{{2k-1}} + \dfrac{1}{{2k + 1}}} \right)} \\&= 1 + \dfrac{2}{3} + \dfrac{2}{5} + \cdots + \dfrac{2}{{2n-1}} + \dfrac{1}{{2n + 1}}.\end{split}$$

如图，上式右边不小于

$$\begin{split} 1 + \dfrac{2}{3} + \int_5^{2n + 2} {\dfrac{1}{x}{\rm d}x} &> \dfrac{5}{3} + \int_5^{2n + 1} {\dfrac{1}{x}{\rm d}x} \\&= \dfrac{5}{3} + \left. {\ln x} \right|_5^{2n + 1} \\&= \ln \left( {2n + 1} \right) + \dfrac{5}{3} - \ln 5> \ln \left( {2n + 1} \right),\end{split}$$ 相当于用第1、2个小矩形来填充区间$\left[ {2 , 3} \right]$上的空白．

利用凹凸性

如图，考虑到$y = \dfrac{1}{x}$为下凸函数，于是有

$$\begin{split} \sum\limits_{k = 1}^n {\dfrac{{4k}}{{4{k^2}-1}}} &= \sum\limits_{k = 1}^n {\left( {\dfrac{1}{{2k-1}} + \dfrac{1}{{2k + 1}}} \right)} \\&> \int_1^{2n + 1} {\dfrac{1}{x}{\rm d}x = \ln \left( {2n + 1} \right)}.\end{split}$$

有关利用凹凸性增加放缩精度的例子还可以参考《积分放缩法》．

最后给出三道练习供读者巩固之用，由于均为证明题，因此答案从略．

练习1、（2012年天津）已知函数$f\left( x \right) = x-\ln \left( {x + a} \right)$的最小值为$0$，其中$a > 0$．

（1）求$a$的值；

（2）若对任意的$x \in \left[ {0 , + \infty } \right)$，有$f\left( x \right) \leqslant k{x^2}$成立，求实数$k$的最小值；

（3）证明：$\sum\limits_{i = 1}^n {\dfrac{2}{{2i-1}}} - \ln \left( {2n + 1} \right) < 2$（$n \in {\mathcal N^ * }$）．

练习2 、（2008年江苏复赛）证明：$\dfrac{1}{{n + 1}} + \dfrac{1}{{n + 2}} + \cdots + \dfrac{1}{{2n}} < \dfrac{{25}}{{36}}$．

练习3 、（2010年湖北）已知函数$f\left( x \right) = ax + \dfrac{b}{x} + c$（$a > 0$）的图象在$\left( {1 , f\left( 1 \right)} \right)$处的切线方程为$y = x-1$．

（1）用$a$表示出$b$，$c$；

（2）若$f\left( x \right) \geqslant \ln x$在$\left[ {1 , + \infty } \right)$上恒成立，求$a$的取值范围；

（3）证明：$1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{n} > \ln \left( {n + 1} \right) + \dfrac{n}{{2\left( {n + 1} \right)}}$（$n \in {\mathcal N^ * }$）．

注    练习2需要用到$\ln 2 < \dfrac{{25}}{{36}}$，证明如下：

由

$$\ln \dfrac{{1 + x}}{{1-x}} = 2\left( {x + \dfrac{{{x^3}}}{3} + \dfrac{{{x^5}}}{5} + \dfrac{{{x^7}}}{7} + \cdots } \right),$$ 取$x = \dfrac{1}{3}$，得 $$\begin{split} \ln 2 &= 2\left( {\dfrac{1}{3} + \dfrac{1}{{{3^3}}} \cdot \dfrac{1}{3} + \dfrac{1}{{{3^5}}} \cdot \dfrac{1}{5} + \dfrac{1}{{{3^7}}} \cdot \dfrac{1}{7} + \cdots } \right) \\&< 2\left( {\dfrac{1}{3} + \dfrac{1}{{{3^4}}} + \dfrac{1}{{{3^6}}} + \dfrac{1}{{{3^8}}} + \cdots } \right) < \dfrac{{25}}{{36}}.\end{split}$$