编者按 本文原作者为刘杨,编辑为意琦行,有大量补充和细节更正.
2011年高考浙江卷理科数学第12题:
已知$x,y\in\mathcal R$,$4x^2+y^2+xy=1$,则$2x+y$的最大值为_______.
解 首先重新叙述问题:
已知$x,y\in\mathcal R$,$x^2+y^2+\dfrac 12xy=1$,求$x+y$的最大值.
解决问题的核心在于如何处理掉交叉项$xy$,有以下不同的思路.
法一 利用均值不等式建立$xy$与$x+y$的联系
根据已知,有$$\begin{split} 1&=x^2+y^2+\dfrac 12xy\\&=(x+y)^2-\dfrac 32xy\\&\geqslant (x+y)^2-\dfrac 32\cdot \left(\dfrac{x+y}{2}\right) ^2\\&=\dfrac 58(x+y)^2,\end{split} $$于是$$x+y\leqslant \sqrt {\dfrac 85}=\dfrac {2\sqrt{10}}5,$$等号当$x=y=\dfrac {\sqrt {10}}5$时取得,因此所求$x+y$的最大值为$\dfrac{2\sqrt{10}}5$.
法二 利用齐次特性创造运用均值不等式的条件
当$xy=0$时,$x+y=\pm 1$;
当$xy\neq 0$时,由于$$\begin{split} (x+y)^2&=\dfrac{x^2+y^2+2xy}{x^2+y^2+\frac 12x y}\\&=1+\dfrac{\frac 32xy}{x^2+y^2+\frac 12xy}\\&=1+\dfrac{\frac 32}{\frac xy+\frac yx+\frac 12}\\&\leqslant 1+\dfrac{\frac 32}{2+\frac 12}=\dfrac 85,\end{split} $$等号当$x=y=\dfrac {\sqrt {10}}5$时取得,因此所求$x+y$的最大值为$\dfrac{2\sqrt{10}}5$.
法三 对二次式进行配方
引入参数,试图使得$$(x+y)^2-\lambda\left(x^2+y^2+\dfrac 12xy\right) $$为完全平方式,即二次式$$(1-\lambda)x^2+\left(2-\dfrac 12\lambda\right) xy+(1-\lambda)y^2$$的判别式$$\Delta=\left(2-\dfrac 12\lambda\right)^2-4(1-\lambda)^2=0,$$解得$\lambda=\dfrac 85$($\lambda=0$舍去),进而可得$x+y$的最大值为$\dfrac{2\sqrt{10}}5$.
法四 利用判别式处理二次式
令$t=x+y$,则$y=t-x$,代入已知条件,整理得$$3x^2-3tx+2t^2-2=0,$$其判别式$$\Delta=-15t^2+24\geqslant 0,$$解得$$-\dfrac{2\sqrt{10}}5 \leqslant t\leqslant \dfrac {2\sqrt {10}}5,$$右边等号当$x=y=\dfrac {\sqrt {10}}5$时取得,因此所求$x+y$的最大值为$\dfrac{2\sqrt{10}}5$.
法五 主元配方后三角换元
将题中条件通过主元配方转化为$$\left(x+\dfrac 14y\right)^2+\left(\dfrac{\sqrt{15}}4y\right)^2=1,$$于是令$$x+\dfrac 14y=\cos\theta,\dfrac{\sqrt{15}}4y=\sin\theta,$$此时$$x+y=\dfrac{3}{\sqrt{15}}\sin\theta+\cos\theta,$$其最大值为$$\sqrt{\left( \dfrac{3}{\sqrt{15}}\right)^2+1^2}=\dfrac{2\sqrt{10}}5,$$等号显然可以取到,于是所求最大值为$\dfrac{2\sqrt{10}}5$.
法六 联想已知条件的几何意义
先考虑$x,y$均为正实数的情形.
由于已知条件的形式,联想余弦定理.将条件改写为$$x^2+y^2-2xy\cdot \left (-\dfrac 14\right) =1,$$于是可以构造$\triangle ABC$,其中$BC=x$,$CA=y$,$AB=1$,角$C$为定角$\arccos\left(-\dfrac 14\right) $.
接下来求$BC+CA$的最大值,有两种不同的途径.
三角途径
由正弦定理,有$$\dfrac{x}{\sin A}=\dfrac{y}{\sin B}=\dfrac{1}{\sin C},$$于是$$\begin{split} x+y&=\dfrac{\sin A+\sin B}{\sin C}\\&=\dfrac{2\sin\frac{A+B}2\cdot\cos\frac{A-B}2}{\sin C}\\&\leqslant \dfrac{2\sin\frac{\pi-C}2}{\sin C}=\dfrac{2\sqrt{10}}5,\end{split} $$当$A=B$,即$x=y=\dfrac{\sqrt{10}}5$时取得等号.
几何途径
直接考虑定线段$AB$所对的角$C$为定角,于是$C$在以$AB$为弦的一段圆弧上.此时求$AC+BC$的最大值不易(需要借助椭圆).
延长$AC$到$D$,使得$CD=CB$,则$\angle ADB$也为定角(为$\arcsin\sqrt{\dfrac{5}{8}}$),于是$D$也在以$AB$为弦的一段圆弧上,此时易得$AD$的最大值为圆弧的直径,为$$\dfrac{AB}{\sin D}=\dfrac{2\sqrt{10}}5,$$当$C$平分$AD$,即$x=y=\dfrac{\sqrt{10}}5$时取得等号,因此所求$x+y$的最大值为$\dfrac{2\sqrt{10}}5$.
接下来证明当$x,y$不均为正实数时$x+y \leqslant \dfrac{2\sqrt{10}}5$:
当$x,y\leqslant 0$时,显然;
当$xy<0$时,有$$(x+y)^2=x^2+y^2+2xy< x^2+y^2+\dfrac 12xy=1,$$于是$$x+y <1<\dfrac{2\sqrt{10}}5.$$
于是所求的最大值为$\dfrac{2\sqrt{10}}5$.
注一 法五中利用三角处理的部分也可以通过柯西不等式进行描述.
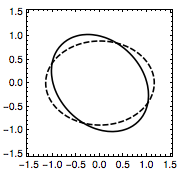
注二 可以利用变换$$\begin{pmatrix} x\\y\end{pmatrix}=\begin{pmatrix}\dfrac{\sqrt 2}2&\dfrac{\sqrt 2}2\\-\dfrac{\sqrt 2}2&\dfrac{\sqrt 2}2\end{pmatrix}\begin{pmatrix}m\\n\end{pmatrix}$$将椭圆$x^2+y^2+\dfrac 12xy=1$旋转$45^\circ$,将其“摆正”为$$\dfrac{3m^2}4+\dfrac{5n^2}4=1,$$如图.
所求$x+y=\sqrt 2n$,其最大值为$\dfrac{2\sqrt{10}}5$.