2015年高考湖北卷理科数学第10题（选择压轴题）：
设\(x\in\mathcal R\)，\([x]\)表示不超过\(x\)的最大整数．若存在实数\(t\)，使得\([t]=1\)，\(\left[t^2\right]=2\)，\(\cdots\)，\(\left[t^n\right]=n\)同时成立，则正整数\(n\)的最大值是（ ）
A．3
B．4
C．5
D．6
2015年高考湖南卷理科数学第21题（压轴题）：
已知\(a>0\)，函数\(f(x)={\rm e}^{ax}\sin x\)（\(x\in [0,+\infty)\)）．记\(x_n\)为\(f(x)\)的从小到大的第\(n\)（\(n\in\mathcal N^*\)）个极值点，证明：
（1）数列\(\left\{f(x_n)\right\}\)是等比数列；
（2）若\(a\geqslant\dfrac{1}{\sqrt{{\rm e}^2-1}}\)，则对一切\(n\in \mathcal N^*\)，\(x_n<\left|f(x_n)\right|\)恒成立．
2015年高考湖南卷理科数学第10题（选择压轴题）、文科数学第10题与之类似：
某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=新工件的体积/原工件的体积）（ ）
A．\(\dfrac 8{9\pi}\)
B．\(\dfrac{16}{9\pi}\)
C．\(\dfrac{4\left(\sqrt 2-1\right)^3}{\pi}\)
D．\(\dfrac{12\left(\sqrt 2-1\right)^3}{\pi}\)
2011年高考山东理科数第22题（压轴题）：
已知动直线\(l\)与椭圆\(C:\dfrac{x^2}{3}+\dfrac{y^2}{2}=1\)交于\(P(x_1,y_1)\)，\(Q(x_2,y_2)\)两个不同点，且三角形\(OPQ\)的面积\(S_{\triangle OPQ}=\dfrac{\sqrt 6}{2}\)，其中\(O\)为坐标原点．
（1）证明：\(x_1^2+x_2^2\)和\(y_1^2+y_2^2\)均为定值；
（2）设线段\(PQ\)的中点为\(M\)，求\(OM\cdot PQ\)的最大值；
（3）椭圆\(C\)上是否存在三点\(D\)、\(E\)、\(G\)，使得\(S_{\triangle ODE}=S_{\triangle ODG}=S_{\triangle OEG}=\dfrac{\sqrt 6}2\)？若存在，判断\(\triangle DEG\)的形状；若不存在，请说明理由．
法一 参数方程
直线\(OP\)的方程为\(y_1x-x_1y=0\)，于是三角形\(OPQ\)的面积\[\begin{split}S_{\triangle OPQ}&=\dfrac 12\sqrt{x_1^2+y_1^2}\cdot\dfrac{\left|x_2y_1-x_1y_2\right|}{\sqrt{x_1^2+x_2^2}}\\&=\dfrac 12\left|x_1y_2-x_2y_1\right|.\end{split}\]设\(P\left(\sqrt 3\cos\alpha,\sqrt 2\sin\alpha\right)\)，\(Q\left(\sqrt 3\cos\beta,\sqrt 2\sin\beta\right)\)代入上式，结合\(S_{\triangle OPQ}=\dfrac{\sqrt 6}{2}\)可得\[\dfrac 12\left|\sqrt 3\cos\alpha\cdot\sqrt 2\sin\beta-\sqrt 2\sin\alpha\cdot\sqrt 3\cos\beta\right|=\dfrac{\sqrt 6}{2},\]化简得\[\sin \left(\alpha-\beta\right)=\pm 1.\]考虑到\(P\)、\(Q\)的对称性，不妨设\(\beta=\alpha+\dfrac\pi 2+2k\pi,k\in\mathcal Z\)，于是有\[\sin\beta=\cos\alpha,\cos\beta=-\sin\alpha.\]
（1）证明 根据上述推导，有\[x_1^2+x_2^2=\left(\sqrt 3\cos\alpha\right)^2+\left(\sqrt 3\cos\beta\right)^2=3,\]且\[y_1^2+y_2^2=\left(\sqrt 2\sin\alpha\right)^2+\left(\sqrt 2\sin\beta\right)^2=2,\]因此命题得证．
（2）解 根据上述推导，有\[M\left(\dfrac{\sqrt 3}{2}\left(\cos\alpha+\cos\beta\right),\dfrac{\sqrt 2}{2}\left(\sin\alpha+\sin\beta\right)\right),\]从而\[\begin{split}OM^2&=\dfrac 34\left(\cos\alpha+\cos\beta\right)^2+\dfrac 12\left(\sin\alpha+\sin\beta\right)^2\\&=\dfrac 34\left(\cos\alpha-\sin\alpha\right)^2+\dfrac 12\left(\sin\alpha+\cos\alpha\right)^2\\&=\dfrac 14\left(5-\sin{2\alpha}\right),\end{split}\]而\[\begin{split}PQ^2&=3\left(\cos\alpha-\cos\beta\right)^2+2\left(\sin\alpha-\sin\beta\right)^2\\&=3\left(\cos\alpha+\sin\alpha\right)^2+2\left(\sin\alpha-\cos\alpha\right)^2\\&=5+\sin{2\alpha},\end{split}\]于是\[OM\cdot PQ=\dfrac 12\sqrt{25-\sin^2{2\alpha}}\leqslant \dfrac 52,\]等号当\(\alpha=0\)时取得．因此\(OM\cdot PQ\)的最大值为\(\dfrac 52\)．
（3）解 不存在．因为不存在\(\alpha,\beta,\gamma\in\mathcal R\)，使得\[\left|\sin\left(\alpha-\beta\right)\right|=1,\\\left|\sin\left(\beta-\gamma\right)\right|=1,\\\left|\sin\left(\gamma-\alpha\right)\right|=1\]同时成立．
法二 仿射变换
利用仿射变换\[\begin{cases}x'=x,\\y'=\dfrac{\sqrt 3}{\sqrt 2}y\end{cases}\]将椭圆\(\dfrac{x^2}{3}+\dfrac{y^2}{2}=1\)拉伸成为圆\(x'^2+y'^2=3\)，此时\[S_{\triangle OP'Q'}=\dfrac{\sqrt 3}{\sqrt 2}\cdot S_{\triangle OPQ}=\dfrac 32,\]于是可知三角形\(OP'Q'\)是以\(P'Q'\)为斜边的直角三角形，如图．
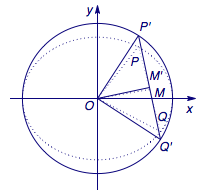（1）证明 注意到\(P'\left(x_1,\dfrac{\sqrt 3}{\sqrt 2}y_1\right)\)，\(Q'\left(x_2,\dfrac{\sqrt 3}{\sqrt 2}y_2\right)\)，且\(OP'\perp OQ'\)，于是有\[x_1^2+x_2^2=\left(\dfrac{\sqrt 3}{\sqrt 2}y_1\right)^2+\left(\dfrac{\sqrt 3}{\sqrt 2}y_2\right)^2=3,\]进而可得\[x_1^2+x_2^2=3,y_1^2+y_2^2=2\]均为定值，命题得证．
（2）解 当直线\(OM\)与直线\(PQ\)的斜率均存在时，设直线\(OM\)的斜率为\(k\)，则根据椭圆的“垂径定理”，可得直线\(PQ\)的斜率为\(-\dfrac{2}{3k}\)，于是根据弦长公式，可得\[\begin{split}OM\cdot PQ&=\dfrac{\sqrt{1+k_{OM}^2}}{\sqrt{1+k_{OM'}^2}}\cdot OM'\cdot\dfrac{\sqrt{1+k_{PQ}^2}}{\sqrt{1+k_{P'Q'}^2}}\cdot P'Q'\\&=\dfrac{\sqrt{1+k^2}}{\sqrt{1+\frac 32k^2}}\cdot OM'\cdot\dfrac{\sqrt{1+\left(-\dfrac{2}{3k}\right)^2}}{\sqrt{1+\frac 32\left(-\dfrac{2}{3k}\right)^2}}\cdot P'Q'\\&=\sqrt{\frac 23+\frac{1}{9(t+2)}}\cdot OM'\cdot P'Q',\end{split}\]其中\(t=\dfrac 32k^2+\dfrac 2{3k^2}\)．
注意到\[\dfrac 12OM'\cdot P'Q'=S_{\triangle OP'Q'}=\dfrac 32,\]于是\[OM'\cdot P'Q'=3,\]又\[t=\dfrac 32k^2+\dfrac 2{3k^2}\geqslant 2,\]等号当\(k^2=\dfrac 23\)时取得，因此有\[\begin{split}OM\cdot PQ&=3\sqrt{\frac 23+\frac{1}{9(t+2)}}\\&\leqslant \dfrac 52,\end{split}\]等号当\(k^2=\dfrac 23\)时取得．
当直线\(OM\)或直线\(PQ\)的斜率不存在时，可计算得\[OM\cdot OQ=\sqrt 6<\dfrac 52.\]
综上，所求最大值为\(\dfrac 52\)．
（3）解 由于圆\(x'^2+y'^2=3\)上的任意三点\(D'\)、\(E'\)、\(G'\)的连线\(D'E'\)、\(E'G'\)、\(D'G'\)对圆心\(O\)的张角不可能同时为直角，于是符合题意的三点\(D\)、\(E\)、\(G\)不存在．
2015年高考福建卷理科数学第20题（压轴题）：
已知函数\(f(x)=\ln (1+x)\)，\(g(x)=kx\)，\(k\in \mathcal R\)．
（1）证明：当\(x>0\)时，\(f(x)<x\)；
（2）证明：当\(k<1\)时，存在\(x_0>0\)，使得对任意\(x\in (0,x_0)\)，恒有\(f(x)>g(x)\)；
（3）确定\(k\)的所有可能取值，使得存在\(t>0\)，对任意\(x\in (0,t)\)，恒有\(\left|f(x)-g(x)\right|<x^2\)．
2015年高考数学浙江理科第15题（填空压轴题）：
已知\({\vec e_1}\)，\(\vec e_2\)是空间单位向量，\({\vec e_1}\cdot {\vec e_2}=\dfrac 12\)．若空间向量\(\vec b\)满足\({\vec b}\cdot{\vec e_1}=2\)，\({\vec b}\cdot{\vec e_2}=\dfrac 52\)，且对于任意\(x,y\in\mathcal R\)，\(\left|{\vec b}-\left(x{\vec e_1}+y{\vec e_2}\right)\right|\geqslant \left|{\vec b}-\left(x_0{\vec e_1}+y_0{\vec e_2}\right)\right|=1\)（\(x_0,y_0\in\mathcal R\)），则\(x_0=\)_______，\(y_0=\)_______，\(\left|\vec b\right|=\)_______．
2015年高考浙江卷理科数学第20题（压轴题）：
已知数列\(\left\{a_n\right\}\)满足\(a_1=\dfrac 12\)且\(a_{n+1}=a_n-a_n^2\)（\(n\in\mathcal N^*\)）．
（1）证明：\(1\leqslant \dfrac{a_n}{a_{n+1}}\leqslant 2\)（\(n\in\mathcal N^*\)）；
（2）设数列\(\left\{a_n^2\right\}\)的前\(n\)项和为\(S_n\)，证明：\(\dfrac{1}{2(n+2)}\leqslant\dfrac{S_n}{n}\leqslant \dfrac{1}{2(n+1)}\)（\(n\in\mathcal N^*\)）．
2015年高考浙江卷理科数学第8题（选择压轴题）：
如图，已知三角形\(ABC\)，\(D\)是\(AB\)的中点，沿直线\(CD\)将三角形\(ACD\)折成三角形\(A'CD\)，所成二面角\(A'-CD-B\)的平面角为\(\alpha\)，则（ ）
A．\(\angle A'DB\leqslant\alpha\)
B．\(\angle A'DB\geqslant \alpha\)
C．\(\angle A'CB\leqslant \alpha\)
D．\(\angle A'CB\geqslant \alpha\)
2015年高考数学安徽卷理科数学第21题（压轴题）：
设函数\(f(x)=x^2-ax+b\)．
（1）讨论函数\(f(\sin x)\)在\(\left(-\dfrac \pi 2,\dfrac\pi 2\right)\)内的单调性，并判断有无极值，有极值时求出极值；
（2）记\(f_0(x)=x^2-a_0x+b_0\)，求函数\(\left|f(\sin x)-f_0(\sin x)\right|\)在\(\left[-\dfrac\pi 2,\dfrac\pi 2\right]\)上的最大值\(D\)；
（3）在（2）中，取\(a_0=b_0=0\)，求\(z=b-\dfrac{a^2}4\)满足\(D\leqslant 1\)时的最大值．
2015年高考数学安徽卷理科第15题（填空压轴题）：
设\(x^3+ax+b=0\)，其中\(a,b\)均为实数，下列条件中，使得该三次方程仅有一个实根的是_______（写出所有正确条件的编号）．
① \(a=-3\)，\(b=-3\)；
② \(a=-3\)，\(b=2\)；
③ \(a=-3\)，\(b>2\)；
④ \(a=0\)，\(b=2\)；
⑤ \(a=1\)，\(b=2\)．
