2015年高考浙江卷理科数学第8题（选择压轴题）：
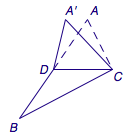
如图，已知三角形\(ABC\)，\(D\)是\(AB\)的中点，沿直线\(CD\)将三角形\(ACD\)折成三角形\(A'CD\)，所成二面角\(A'-CD-B\)的平面角为\(\alpha\)，则（ ）
A．\(\angle A'DB\leqslant\alpha\)
B．\(\angle A'DB\geqslant \alpha\)
C．\(\angle A'CB\leqslant \alpha\)
D．\(\angle A'CB\geqslant \alpha\)
正确答案是B．
得到答案是容易的，可以取以下两种极端情形进行排除：
当\(\alpha=\pi\)时，显然\(\angle A'DB=\angle ADB=\pi\)，而\(\angle A'CB=\angle ACB<\pi\)，排除D；
当\(\alpha=0\)时，显然\(\angle A'DB=\angle A'^\prime DB>0\)，而\(\angle A'CB=\angle A'^\prime CB>0\)，排除A、C．
下面证明选项B是正确的．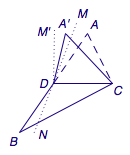
如图，在平面\(ABC\)内过\(D\)作线段\(MN\)垂直于\(CD\)，且\(AB=MN\)，\(D\)亦为\(MN\)的中点．设在折叠过程中，\(M\)的对应点为\(M'\)，则根据二面角的平面角的定义有\(\alpha=\angle M'DN\)．
若线段\(MN\)与线段\(AB\)重合，那么就有\(\angle M'DN=\angle A'DB\)，命题成立；
若线段\(MN\)不于线段\(AB\)重合，那么\(A\)和\(B\)分别位于直线\(MN\)两侧，于是\(A'\)和\(B\)分别位于平面\(M'DN\)两侧．进而在三角形\(A'DB\)和三角形\(M'DB\)中，\(M'D=A'D\)且\(BA'>BM'\)，于是\(\angle A'DB>\angle M'DB\)．而在三角形\(M'DB\)和三角形\(M'DN\)中，\(DN=DB\)且\(M'B>M'N\)，于是\(\angle M'DB>\angle M'DN\)，于是命题成立．
注 也可以利用三射线定理\[\cos\angle A'DB=\cos\angle A'DC\cos\angle BDC+\sin\angle A'DC\sin\angle BDC\cos\alpha,\]结合\(\angle A'DC+\angle BDC=\pi\)，有\[1+\cos\angle A'DB=\left(1+\cos\alpha\right)\cdot\sin\angle A'DC\sin\angle BDC,\]因此\[\cos\angle A'DB\leqslant \cos\alpha,\]考虑到余弦函数在\([0,\pi]\)内单调递减，于是命题成立．