Math173

1、甲、乙、丙三人玩传球游戏，第\(1\)次由甲将球传出，传了\(4\)次球后，球回到甲手里的方案数为_______．

2、求证：数列\(a_n=\left(1+\dfrac 1n\right)^{n+1}\)单调递减．

3、已知\(p\)是一个不为\(2\)的质数，求证：将\(\dfrac 2p\)拆分为两个不同的正整数的倒数之和的方式存在且唯一．

4、平面直角坐标系内，若一个圆的圆心的横坐标和纵坐标均为无理数，求证：该圆上不可能存在\(3\)个整点（横坐标和纵坐标均为整数的点）．

继续阅读 →

一、选择题

选择题共5小题；在每小题的四个选项中，只有一项符合题目要求，把正确选项的代号填在括号中，选对得10分，选错扣5分，不选得0分．

1、已知$n$为不超过$2015$的正整数且$1^n+2^n+3^n+4^n$的个位数为$0$，则满足条件的正整数$n$的个数为（        ）

A．$1511$

B．$1512$

C．$1513$

D．前三个答案都不对

继续阅读 →

说明：本试卷共30小题，共100分．在每小题给出的四个选项中，有一个或多个选项是符合题目要求的．全部选对的，得满分；选对但不全的，得部分分；有选错的，得0分．

1、设复数$z=\cos\dfrac{2\pi}3+{\rm i}\sin\dfrac{2\pi}3$，则$\dfrac{1}{1-z}+\dfrac{1}{1-z^2}=$（        ）

A．$0$

B．$1$

C．$\dfrac 12$

D．$\dfrac 32$

2、设$\{a_n\}$为等差数列，$p,q,k,l$为正整数，则“$p+q>k+l$”是“$a_p+a_q>a_k+a_l$”的（        ）

A．充分不必要条件

B．必要不充分条件

C．充分必要条件

D．既不充分也不必要条件

3、设$A,B$是抛物线$y=x^2$上的两点，$O$是坐标原点．若$OA\perp OB$，则（        ）

A．$|OA|\cdot |OB|\geqslant 2$

B．$|OA|+|OB|\geqslant 2\sqrt 2$

C．直线$AB$过抛物线$y=x^2$的焦点

D．$O$到直线$AB$的距离小于等于$1$

4、设函数$f(x)$的定义域为$(-1,1)$，且满足：

① $f(x)>0$，$x\in(-1,0)$；

② $f(x)+f(y)=f\left(\dfrac{x+y}{1+xy}\right)$，$x,y\in(-1,1)$，

则$f(x)$为（        ）

A．奇函数

B．偶函数

C．减函数

D．有界函数

5、如图，已知直线$y=kx+m$与曲线$y=f(x)$相切于两点，则$F(x)=f(x)-kx$有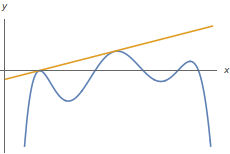（        ） A．$2$个极大值点

B．$3$个极大值点

C．$2$个极小值点

D．$3$个极小值点

6、$\triangle ABC$的三边分别为$a,b,c$．若$c=2$，$\angle C=\dfrac{\pi}3$，且$$\sin C+\sin (B-A)-2\sin 2A=0,$$则（        ）

A．$b=2a$

B．$\triangle ABC$的周长为$2+2\sqrt 3$

C．$\triangle ABC$的面积为$\dfrac{2\sqrt 3}3$

D．$\triangle ABC$的外接圆半径为$\dfrac{2\sqrt 3}3$

7、设函数$f(x)=\left(x^2-3\right){\rm e}^x$，则（        ）

A．$f(x)$有极小值，但无最小值

B．$f(x)$有极大值，但无最大值

C．若方程$f(x)=b$恰有一个实根，则$b>\dfrac{6}{{\rm e}^3}$

D．若方程$f(x)=b$恰有三个不同实根，则$0<b<\dfrac{6}{{\rm e}^3}$

8、已知$A=\left\{(x,y)\left|x^2+y^2=r^2\right.\right\}$，$B=\left\{(x,y)\left|(x-a)^2+(y-b)^2=r^2\right.\right\}$，已知$A\cap B=\left\{(x_1,y_1),(x_2,y_2)\right\}$，则（        ）

A．$0<a^2+b^2<2r^2$

B．$a(x_1-x_2)+b(y_1-y_2)=0$

C．$x_1+x_2=a$，$y_1+y_2=b$

D．$a^2+b^2=2ax_1+2by_1$

9、已知非负实数$x,y,z$满足$4x^2+4y^2+z^2+2z=3$，则$5x+4y+3z$的最小值为（        ）

A．$1$

B．$2$

C．$3$

D．$4$

10、设数列$\{a_n\}$的前$n$项和为$S_n$，若对任意正整数$n$，总存在正整数$m$，使得$S_n=a_m$，则（        ）

A．$\{a_n\}$可能为等差数列

B．$\{a_n\}$可能为等比数列

C．$\{a_n\}$的任意一项均可写成$\{a_n\}$的两项之差

D．对任意正整数$n$，总存在正整数$m$，使得$a_n=S_m$

11、运动会上，有$6$名选手参加$100$米比赛，观众甲猜测：$4$道或$5$道的选手得第一名；观众乙猜测：$3$道的选手不可能得第一名；观众丙猜测：$1,2,6$道选手中的一位获得第一名；观众丁猜测：$4,5,6$道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有$1$人猜对比赛结果，此人是（        ）

A．甲

B．乙

C．丙

D．丁

12、长方体$ABCD-A_1B_1C_1D_1$中，$AB=2$，$AD=AA_1=1$，则$A$到平面$A_1BD$的距离为（        ）

A．$\dfrac 13$

B．$\dfrac 23$

C．$\dfrac{\sqrt 2}2$

D．$\dfrac{\sqrt 6}3$

13、设不等式组$\begin{cases} |x|+|y|\leqslant 2,\\ y+2\leqslant k(x+1),\end{cases} $所表示的区域为$D$，其面积为$S$，则（        ）

A．若$S=4$，则$k$的值唯一

B．若$S=\dfrac 12$，则$k$的值有$2$个

C．若$D$为三角形，则$0<k\leqslant \dfrac 23$

D．若$D$为五边形，则$k>4$

14、$\triangle ABC$的三边长是$2,3,4$，其外心为$O$，则$\overrightarrow{OA}\cdot \overrightarrow{AB}+\overrightarrow{OB}\cdot\overrightarrow{BC}+\overrightarrow{OC}\cdot\overrightarrow{CA}=$（        ）

A．$0$

B．$-15$

C．$-\dfrac{21}2$

D．$-\dfrac{29}2$

15、设随机事件$A$与$B$互相独立，且$P(B)=0.5$，$P(A-B)=0.2$，则（         ）

A．$P(A)=0.4$

B．$P(B-A)=0.3$

C．$P(AB)=0.2$

D．$P(A+B)=0.9$

16、过$\triangle ABC$的重心作直线将$\triangle ABC$分成两部分，则这两部分的面积之比的（        ）

A．最小值为$\dfrac 34$

B．最小值为$\dfrac 45$

C．最大值为$\dfrac 43$

D．最大值为$\dfrac 54$

17、从正$15$边形的顶点中选出$3$个构成钝角三角形，则不同的选法有（        ）

A．$105$种

B．$225$种

C．$315$种

D．$420$种

18、已知存在实数$r$，使得圆周$x^2+y^2=r^2$上恰好有$n$个整点，则$n$可以等于（        ）

A．$4$

B．$6$

C．$8$

D．$12$

19、设复数$z$满足$2|z|\leqslant |z-1|$，则（        ）

A．$|z|$的最大值为$1$

B．$|z|$的最小值为$\dfrac 13$

C．$z$的虚部的最大值为$\dfrac 23$

D．$z$的实部的最大值为$\dfrac 13$

20、设$m,n$是大于零的实数，向量${\bf a}=(m\cos\alpha,m\sin\alpha)$，${\bf b}=(n\cos\beta,n\sin\beta)$，其中$\alpha,\beta\in [0,2\pi)$．定义向量${\bf a}^{\frac 12}=\left(\sqrt m\cos\dfrac{\alpha}2,\sqrt m\sin\dfrac{\alpha}2\right)$，${\bf b}^{\frac 12}=\left(\sqrt n\cos\dfrac{\beta}2,\sqrt n\sin\dfrac{\beta}2\right)$，记$\theta=\alpha-\beta$，则（        ）

A．${\bf a}^{\frac 12}\cdot{\bf a}^{\frac 12}={\bf a}$

B．${\bf a}^{\frac 12}\cdot {\bf b}^{\frac 12}=\sqrt{mn}\cos\dfrac{\theta}2$

C．$\left|{\bf a}^{\frac 12}-{\bf b}^{\frac 12}\right|^2\geqslant 4\sqrt{mn}\sin^2\dfrac{\theta}4$

D．$\left|{\bf a}^{\frac 12}+{\bf b}^{\frac 12}\right|^2\geqslant 4\sqrt{mn}\cos^2\dfrac{\theta}4$

21、设数列$\{a_n\}$满足：$a_1=6$，$a_{n+1}=\dfrac{n+3}na_n$，则（        ）

A．$\forall n\in\mathcal N^*,a_n<(n+1)^3$

B．$\forall n\in\mathcal N^*,a_n\neq 2015$

C．$\exists n\in\mathcal N^*,a_n$为完全平方数

D．$\exists n\in\mathcal N^*,a_n$为完全立方数

22、在极坐标系中，下列方程表示的图形是椭圆的有（        ）

A．$\rho=\dfrac{1}{\cos\theta+\sin\theta}$

B．$\rho=\dfrac{1}{2+\sin\theta}$

C．$\rho=\dfrac{1}{2-\cos\theta}$

D．$\rho=\dfrac{1}{1+2\sin\theta}$

23、设函数$f(x)=\dfrac{\sin\pi x}{x^2-x+1}$，则（        ）

A．$f(x)\leqslant \dfrac 43$

B．$\left|f(x)\right|\leqslant 5|x|$

C．曲线$y=f(x)$存在对称轴

D．曲线$y=f(x)$存在对称中心

24、$\triangle ABC$的三边分别为$a,b,c$，若$\triangle ABC$为锐角三角形，则（        ）

A．$\sin A>\cos B$

B．$\tan A>\cot B$

C．$a^2+b^2>c^2$

D．$a^3+b^3>c^3$

25、设函数$f(x)$的定义域是$(-1,1)$，若$f(0)=f'(0)=1$，则存在实数$\delta\in (0,1)$，使得（        ）

A．$f(x)>0$，$x\in(-\delta,\delta)$

B．$f(x)$在$(-\delta,\delta)$上单调递增

C．$f(x)>1$，$x\in(0,\delta)$

D．$f(x)>1$，$x\in(-\delta,0)$

26、在直角坐标系中，已知$A(-1,0)$，$B(1,0)$．若对于$y$轴上的任意$n$个不同点$P_1,P_2,\cdots ,P_n$，总存在两个不同点$P_i,P_j$，使得$\left|\sin\angle AP_iB-\sin \angle AP_jB\right|\leqslant \dfrac 13$，则$n$的最小值为（        ）

A．$3$

B．$4$

C．$5$

D．$6$

27、设非负实数$x,y$满足$2x+y=1$，则$x+\sqrt{x^2+y^2}$的（        ）

A．最小值为$\dfrac 45$

B．最小值为$\dfrac 25$

C．最大值为$1$

D．最大值为$\dfrac{1+\sqrt 2}3$

28、对于$50$个黑球和$49$个白球的任意排列（从左到右排成一行），则（        ）

A．存在一个黑球，它右侧的白球和黑球一样多

B．存在一个白球，它右侧的白球和黑球一样多

C．存在一个黑球，它右侧的白球比黑球少一个

D．存在一个白球，它右侧的白球比黑球少一个

29、从$1,2,3,4,5$中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如$12231$，则能得到的不同的五位数有（        ）

A．$300$个

B．$450$个

C．$900$个

D．$1800$个

30、设曲线$L$的方程为$y^4+\left(2x^2+2\right)y^2+\left(x^4-2x^2\right)=0$，则（        ）

A．$L$是轴对称图形

B．$L$是中心对称图形

C．$L\subset\left\{(x,y)\left|x^2+y^2\leqslant 1\right.\right\}$

D．$L\subset\left\{(x,y)\left|-\dfrac 12\leqslant y\leqslant \dfrac 12\right.\right\}$

 

---

参考答案

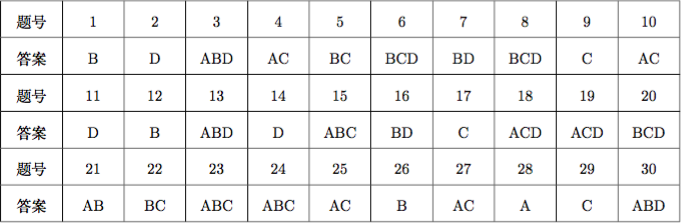
点击此处下载pdf．