2015年高考四川卷理科数学第21题（压轴题）：
已知函数\(f(x)=-2(x+a)\ln x+x^2-2ax-2a^2+a\)，其中\(a>0\)．
（1）设\(g(x)\)是\(f(x)\)的导函数，讨论\(g(x)\)的单调性；
（2）证明：存在\(a\in (0,1)\)，使得\(f(x)\geqslant 0\)在区间\((1,+\infty)\)内恒成立，且\(f(x)=0\)在区间\((1,+\infty)\)内有唯一解．
（1）解 根据已知，有\[g(x)=f'(x)=-2\ln x+2x-2-\dfrac{2a}{x}-2a,\]于是\[g'(x)=\dfrac{2}{x^2}\left(x^2-x+a\right),\]因此
当\(0<a<\dfrac 14\)时，\(g(x)\)在\(\left(0,\dfrac{1-\sqrt{1-4a}}2\right)\)上单调递增，在\(\left(\dfrac{1-\sqrt{1-4a}}2,\dfrac{1+\sqrt{1-4a}}{2}\right)\)上单调递减，在\(\left(\dfrac{1+\sqrt{1-4a}}2,+\infty\right)\)上单调递增；
当\(a\geqslant \dfrac 14\)时，\(g(x)\)在\(\mathcal R^+\)上单调递增．
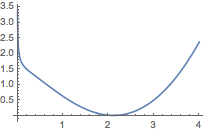
（2）证明 根据题意，函数\(f(x)\)的图象应该如图所示．
考虑函数\(g(x)\)，由于\(g'(1)=2a>0\)，于是在\((1,+\infty)\)上\(g(x)\)单调递增．又\(g(1)=-4a<0\)，\(g(+\infty)>0\)，于是\(f(x)\)在\((1,+\infty)\)上先单调递减，再单调递增，有极小值点．设\(f(x)\)的极小值点为\(x=x_0\)，则\[\begin{cases}-\ln x_0+x_0-1-a\left(\dfrac 1{x_0}+1\right)=0,\\-2(x_0+a)\ln x_0+x_0^2-2ax_0-2a^2+a=0,\end{cases}\]我们的目标是证明这个二元方程组有实数解，且至少有一组解满足限制条件\[x_0>1\land 0<a<1.\]
采用消元的策略，由第一个方程可得\[a=\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1},\]代入第二个方程有\[-2\left(x_0+\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1}\right)\ln x_0+x_0^2-2x_0\cdot \dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1}-2\left(\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1}\right)^2+\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1}=0,\]记该方程左边为\(\varphi (x_0)\)，则\[\varphi (1)=1>0,\]且\[\begin{split}\varphi ({\rm e})&=\left({\rm e-2}\right)\left[-\dfrac{1}{{\rm e}^{-1}+1}-2\dfrac {{\rm e}-2}{\left( {\rm e}^{-1}+1\right)^2}\right]\\&<0,\end{split}\]因此必然存在\(x_0\in (1,{\rm e})\)，使得\(\varphi (x_0)=0\)．
此时\[a=\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1},\]记该方程右边为\(\mu (x_0)\)，则\[\mu' (x_0)=\dfrac{x_0^2+x_0-2-\ln x_0}{(1+x_0)^2},\]当\(x_0\in (1,{\rm e})\)时，函数\(\mu (x_0)\)单调递增（如上图），于是\[0<a<\dfrac{{\rm e}-2}{{\rm e}^{-1}+1}<1,\]因此原命题得证．
2015年10月31日补充练习题，2015年高考全国新课标I卷文科数学第21题（压轴题）：
设函数$f(x)={\rm e} ^{2x}-a\ln x$．
（1）讨论$f(x)$的导函数$f'(x)$的零点的个数；
（2）证明：当$a>0$时，$f(x)\geqslant 2a+a\ln\dfrac 2a$．
答案：（1）$a\leqslant 0$时没有零点，$a>0$时有一个零点；
（2）略．（提示：用极值点坐标表示$a$）