这是我在QQ群高中数学试题研究中看到的一道题目：
已知函数$f(x)=\dfrac ax-x$，对任意$x\in (0,1)$，有$f(x)\cdot f(1-x)\geqslant 1$恒成立，则实数$a$的取值范围为_______．
2012年高考辽宁卷理科数学第11题：
设函数$f(x)$（$x\in\mathcal R$）满足$f(-x)=f(x)$，$f(x)=f(2-x)$，且当$x\in [0,1]$时，$f(x)=x^3$．又函数$g(x)=|x\cos (\pi x)|$，则函数$h(x)=g(x)-f(x)$在$\left[-\dfrac 12,\dfrac 32\right]$上的零点个数为（ ）
A．$5$
B．$6$
C．$7$
D．$8$
对角线互相垂直的四边形四条边有什么等量关系？ 
如图，四边形\(ABCD\)中，若\(AC\perp BD\)，则\(AB^2+CD^2=AD^2+BC^2\)．
如图，已知\(AB=10\)，点\(M\)是线段\(AB\)上的动点，分别以\(AM,BM\)为边，在线段\(AB\)的同侧作等边三角形\(ACM\)和\(MDB\)，连接\(CD\)，设\(CD\)的中点为\(N\)，那么当点\(M\)从点\(A\)运动到点\(B\)时，点\(N\)到线段\(AB\)的距离是怎样变化的？求出点\(N\)的路径长．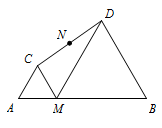
继续阅读
函数的性质本质上指当自变量满足某些关系时，函数值是否随之满足某些关系．具有某种性质的函数，会同时反应在函数的解析式与函数的图象上，借助于性质的本质，解析式满足的关系与图象满足的特征之间可以很好地对应起来．
平面直角坐标系中，\(A(2\sqrt 2,2)\)，点\(Q\)是\(y\)轴上的动点，求\(AQ+\dfrac 13QO\)的最小值． 继续阅读
已知函数$f(x)=a\ln x+\dfrac 1x+\dfrac 1{2x^2}$，$a\in\mathcal R$．
（1）讨论函数$f(x)$的单调性；
（2）证明：$(x-1)\left({\rm e} ^{-x}-x\right)+2\ln x<\dfrac 23$．
