2012年高考辽宁卷理科数学第11题:
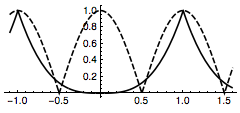
设函数$f(x)$($x\in\mathcal R$)满足$f(-x)=f(x)$,$f(x)=f(2-x)$,且当$x\in [0,1]$时,$f(x)=x^3$.又函数$g(x)=|x\cos (\pi x)|$,则函数$h(x)=g(x)-f(x)$在$\left[-\dfrac 12,\dfrac 32\right]$上的零点个数为( )
A.$5$
B.$6$
C.$7$
D.$8$
正确答案是 B.
下面是一个典型的错解,很多教辅书都是这样给出的解答:
根据题意,$f(x)$是偶函数,同时也是周期为$2$的函数.
显然$x=0$是函数的一个零点;
当$x \ne 0$且$x$在一个周期区间$[-1,1]$上时,函数$h(x)=g(x)-f(x)$的零点,即方程$$|\cos (\pi x)|=\dfrac{f(x)}x,$$考虑到左侧函数周期为$1$,而右侧函数周期为$2$,于是所求区间$\left[-\dfrac 12,\dfrac 32\right]\setminus\{0\}$等价于$\left(-1,1\right]\setminus\{0\}$.
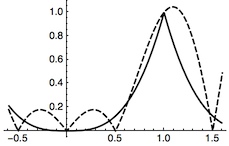
考虑到图形的对称性,只需要考虑$m(x)=x^2$的图象与$n(x)=|\cos (\pi x)|$的图象在区间$\left(0,1\right]$上的交点个数即可.
在区间$\left(0,\dfrac 12\right]$上,$m(x)$单调递增,$n(x)$单调递减,又$$m(0)-n(0)<0,m\left(\dfrac 12\right)-n\left(\dfrac 12\right)>0,$$于是函数$h(x)$在该区间上有$1$个零点;
在区间$\left(\dfrac 12,1\right]$上,注意到$m(x)$下凸递增,$n(x)$上凸递增,又$$m\left(\dfrac 12\right)-n\left(\dfrac 12\right)>0,m(1)-n(1)=0,$$于是函数$h(x)$在该区间上有$2$个零点;
根据对称性,函数$h(x)$在区间$\left(-1,0\right)$上有$2$个零点.
综上,$h(x)$在$\left[-\dfrac 12,\dfrac 32\right]$上有$6$个零点.
错误的原因是
虽然$f(x)$是周期函数,但是$\dfrac{f(x)}x$并非周期函数!
因此这个解法在区间$\left[-\dfrac 12,1\right]$上的讨论都是正确的,在该区间上的零点个数为$5$,我们只需要讨论在$\left(1,\dfrac 32\right] $上的零点个数.
事实上此时$$f(x)-g(x)=(2-x)^3+x\cos (\pi x),$$其导函数$$\left(f(x)-g(x)\right)'=-3(2-x)^2+\cos (\pi x)- \pi x\sin (\pi x),$$二阶导函数为$$\left(f(x)-g(x)\right)''=6(2-x)-2\pi \sin(\pi x)- \pi^2 x\cos (\pi x)>0,$$因此$\left(f(x)-g(x)\right)'$单调递增,从而$$\left(f(x)-g(x)\right)'\left|\right._{x=1}<0,\left(f(x)-g(x)\right)'|_{x=\frac 12}>0,$$进而$f(x)-g(x)$在区间\(\left(1,\dfrac 32\right]\)上先减后增,而$$\left(f(x)-g(x)\right)|_{x=1}=0,\left(f(x)-g(x)\right)|_{x=\frac 12}>0,$$可以断定函数$h(x)$在区间$\left(1,\dfrac 32\right] $上有$1$个零点.
综上,$h(x)$在$\left[-\dfrac 12,\dfrac 32\right]$上有$6$个零点.