解析几何解题技巧之“垂径定理”

        我们都知道垂径定理是圆的重要性质，其内容为：

已知圆中有一条非直径的弦，那么这条弦垂直于过其中点的直径．

        对于椭圆也有类似的性质，我们称之为椭圆的“垂径定理”，描述如下：

已知不过原点$O$的直线与椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$交于$A$、$B$两点，$M$为弦$AB$的中点，则直线$AB$与直线$OM$的斜率之积

$$k_{AB}\cdot k_{OM}=-\dfrac{b^2}{a^2}.$$

注一    当$a=b=r$时，椭圆的垂径定理描述的内容即为圆的垂径定理；

注二    这里并不要求$a>b$，也就是说此结论对焦点在$x$轴和焦点在$y$轴上的椭圆均适用；

注三    双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$的垂径定理中的斜率之积

$$k_{AB}\cdot k_{OM}=\dfrac{b^2}{a^2}.$$

---

         点差法是证明这一性质的最好方法：

设$A\left(x_1,y_1\right)$，$B\left(x_2,y_2\right)$，则

$$\begin{split}\dfrac{x_1^2}{a^2}+\dfrac{y_1^2}{b^2}=1\\\dfrac{x_2^2}{a^2}+\dfrac{y_2^2}{b^2}=1\end{split}$$ 两式相减，有 $$\dfrac{x_1^2-x_2^2}{a^2}+\dfrac{y_1^2-y_2^2}{b^2}=0,$$ 两边同时除以$x_1^2-x_2^2$，并化简可得 $$\dfrac{y_1^2-y_2^2}{x_1^2-x_2^2}=-\dfrac{b^2}{a^2},$$ 利用平方差公式变形，有 $$\dfrac{y_1-y_2}{x_1-x_2}\cdot \dfrac{\dfrac{y_1+y_2}2-0}{\dfrac{x_1+x_2}2-0}=-\dfrac{b^2}{a^2},$$ 此即欲证性质．

---

         证明这一性质的方法，以及这一性质都是解析几何重点学习和掌握的内容．下面就举例说明这一性质的应用．

---

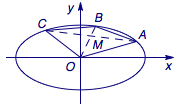
 例1、（2013年北京高考数学理）已知$A,B,C$是椭圆$W:\dfrac{x^2}4+y^2=1$上的三个点，$O$为坐标原点．

（1）当$B$是$W$的右顶点，且四边形$OABC$为菱形时，求此菱形的面积；

（2）当点$B$不是$W$的顶点时，判断四边形$OABC$是否可能是菱形，并说明理由．

---

解    （1）菱形的面积为$\sqrt 3$；

（2）四边形$OABC$不可能为菱形．用反证法证明如下：

假设四边形$OABC$是菱形．当点$B$不是$W$的顶点时，直线$OB$和直线$AC$的斜率都存在，设$OB$与$AC$相交于点$M$，则$M$平分$AC$．

由椭圆的垂径定理得

$$k_{AC}\cdot k_{OM}=-\dfrac 14,$$ 于是$AC$与$OM$不垂直，与四边形$OABC$是菱形矛盾．

因此四边形$OABC$不可能为菱形．

---

例2、（2014年北京东城一模）已知椭圆$G:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$过点$A\left(1,\dfrac{\sqrt 6}3\right)$和$B(0,-1)$．

（1）求椭圆$G$的方程；

（2）设过点$P\left(0,\dfrac 32\right)$的直线$l$与椭圆$G$交于$M$、$N$两点，且$BM=BN$．求直线$l$的方程．

---

 解    （1）$\dfrac{x^2}3+y^2=1$；

（2）设弦$MN$的中点$E$的坐标为$(m,n)$．

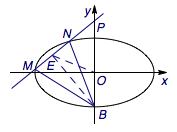由椭圆的垂径定理与已知条件，有

$$\begin{cases}k_{BE}\cdot k_{PE}=-1\\k_{OE}\cdot k_{PE}=-\dfrac 13\end{cases}$$ 于是 $$\begin{cases}\dfrac{\dfrac 32-n}{0-m}\cdot\dfrac{n+1}{m}&=-1\\\dfrac{n}{m}\cdot\dfrac{n-\dfrac 32}{m}&=-\dfrac 13\end{cases}$$ 解得 $$\begin{cases}m=\pm\dfrac{\sqrt 6}2\\n=\dfrac 12\end{cases}$$ 于是直线$l$的方程为 $$y=\pm\dfrac{\sqrt 6}3x+\dfrac 32.$$

---

         友情提示，在考试的时候如果应用了椭圆的垂径定理，记得用点差法叙述一下证明过程哦！

        最后给出一组练习题．

---

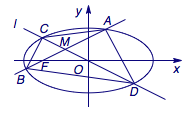
练习1、（2014年北京丰台二模）如图，已知椭圆$E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$的离心率为$\dfrac{\sqrt 3}2$，过左焦点$F\left(-\sqrt 3,0\right)$且斜率为$k$的直线交椭圆$E$于$A$、$B$两点，线段$AB$的中点为$M$，直线$l:x+4ky=0$交椭圆于$C$、$D$两点．

（1）求椭圆$E$的方程；

（2）求证：点$M$在直线$l$上；

（3）是否存在实数$k$，使得三角形$BDM$的面积是三角形$ACM$面积的$3$倍？若存在，求出$k$的值；若不存在，说明理由．

练习2、（2015年北京海淀高三期末文科）已知椭圆$M:x^2+2y^2=2$．

（1）求$M$的离心率及长轴长；

（2）设过椭圆$M$的上顶点$A$的直线$l$与椭圆$M$的另一个交点为$B$，线段$AB$的垂直平分线交椭圆于$C$、$D$两点．问：是否存在直线$l$使得$C$、$O$、$D$三点共线（$O$为坐标原点）？若存在，求出所有满足条件的直线$l$的方程；若不存在，说明理由．

---

参考答案

练习1、（1）$E:\dfrac{x^2}4+y^2=1$；（2）略；（3）存在，$k=\pm\dfrac 12$．

练习2、（1）$e=\dfrac{\sqrt 2}2$，长轴长为$2\sqrt 2$；（2）$l:x=0$．

更多的例题和练习可以参考一般圆锥曲线的“垂径定理”．