每日一题[367]椭圆与矩形

本题改编自2013年北京高考理科数学第19题：

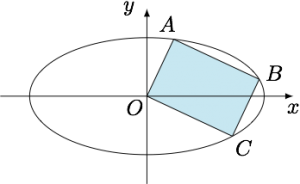
设$A,B,C$是椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$上的三个点，判断四边形$OABC$能否为矩形．

分析    2013年北京高考理科数学第19题中给定$B$不为椭圆的顶点，判断四边形$OABC$能否为菱形．由椭圆的“垂径定理”可以给出否定的结果．对于这道改编题，依然从点的坐标入手思考．

解答    设$A(x_1,y_1)$，$C(x_2,y_2)$，则取$B(x_1+x_2,y_1+y_2)$即可保证四边形$OABC$为平行四边形，因此只需要用条件$$x_1x_2+y_1y_2=0$$表示$\angle AOC$为直角即可．

这样问题就转化为了方程组$$\begin{cases} \dfrac{x_1^2}{a^2}+\dfrac{y_1^2}{b^2}=1,\\ \dfrac{x_2^2}{a^2}+\dfrac{y_2^2}{b^2}=1,\\ \dfrac{(x_1+x_2)^2}{a^2}+\dfrac{(y_1+y_2)^2}{b^2}=1,\\ x_1x_2+y_1y_2=0\end{cases} $$是否有实数解的问题．

展开第三个方程，将其他三个方程代入，可以整理得$$x_1x_2=\dfrac{a^2b^2}{2(a^2-b^2)}.$$

显然直线$OA$和$OC$的斜率均存在，分别设为$k,-\dfrac 1k$，则通过联立直线与椭圆的方程可得$$x_1^2=\dfrac{a^2b^2}{a^2k^2+b^2},x_2^2=\dfrac{a^2b^2k^2}{a^2+b^2k^2},$$因此$$\dfrac{a^2b^2}{a^2k^2+b^2}\cdot\dfrac{a^2b^2k^2}{a^2+b^2k^2}=\left(\dfrac{a^2b^2}{2(a^2-b^2)}\right)^2,$$即$$k^4-\left[3\left(\dfrac{a^2}{b^2}+\dfrac{b^2}{a^2}\right)-8\right]\cdot k^2+1=0,$$该方程有解等价于$$\left[3\left(\dfrac{a^2}{b^2}+\dfrac{b^2}{a^2}\right)-8\right]^2-4\geqslant 0,$$也即$$a^2\geqslant 3b^2.$$因此当椭圆的离心率不小于$\dfrac{\sqrt 6}3$时，四边形$OABC$可能为矩形，如图．

注    当椭圆的离心率为$\dfrac{\sqrt 6}3$时，矩形$OABC$恰好为正方形．