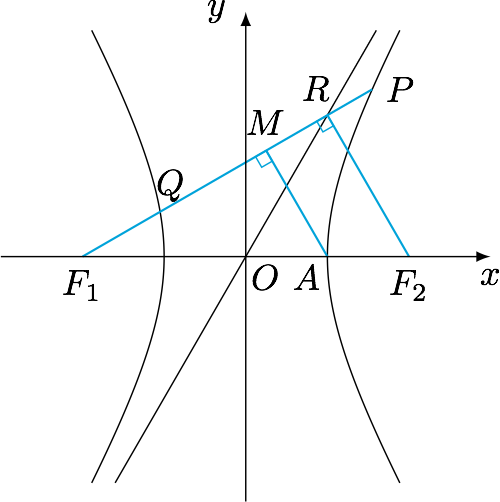
如图,双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$($a,b>0$)的右顶点为$A$,左右焦点分别为$F_1,F_2$,点$P$是双曲线右支上一点,$PF_1$交左支于点$Q$,交渐近线$y=\dfrac bax$于点$R$,$M$是$PQ$的中点,若$RF_2\perp PF_1$,且$AM\perp PF_1$,则双曲线的离心率为_______.
分析 题中条件为一个中点加两组垂直,其中$F_2R\perp RF_1$通过直角三角形的斜边中线转化为$OR=\dfrac 12F_1F_2=c$,其中$c$为双曲线的半焦距.又由于$R$在渐近线上,于是$R$的坐标为$(a,b)$.接下来的关键是如何恰当的表达中点,这就用到了双曲线的“垂径定理”.
解 直线$PF_1$的斜率为$\dfrac{b}{a+c}$,设$M(m,n)$,则$$\begin{cases} \dfrac nm\cdot \dfrac{b}{a+c}=\dfrac{b^2}{a^2},\\ \dfrac{n}{m-a}\cdot\dfrac{b}{a+c}=-1,\\ \dfrac{n}{m+c}=\dfrac{b}{a+c},\end{cases} $$其中第一个方程来源于双曲线的“垂径定理”.
第一个式子与第二个式子相除,可得$$\dfrac{m-a}{m}=-\dfrac{b^2}{a^2},$$即$$m=\dfrac{a^3}{c^2}.$$第一个式子与第三个式子相除,可得$$\dfrac{m+c}{m}\cdot\dfrac{b}{a+c}=\dfrac{b^2}{a^2}\cdot\dfrac{a+c}b,$$将$m=\dfrac{a^3}{c^2}$代入,并整理可得$$e^2-e-2=0,$$于是$e=2$,其中$e=\dfrac ca$为双曲线的离心率.