1、已知方程\(\dfrac{|\cos x|}{x}=k\)在\((0,+\infty)\)上有两个不同的解\(a\),\(b\)(\(a<b\)),则下列四个命题中正确的是( )
A.\(\sin 2a=2a\cos^2a\)
B.\(\cos 2a=2b\sin^2a\)
C.\(\sin 2b=-2b\sin^2b\)
D.\(\cos 2b=-2b\sin^2b\)
2、设\(O\)是正三棱锥\(P-ABC\)底面三角形\(ABC\)的中心,过\(O\)的动平面与\(PC\)交于\(X\),与\(PA\)、\(PB\)的延长线分别交于\(Y\)、\(Z\)两点,则\(\dfrac{1}{PX}+\dfrac{1}{PY}+\dfrac{1}{PZ}\)( )
A.有最大值但无最小值
B.有最小值但无最大值
C.既无最大值也无最小值
D.是定值
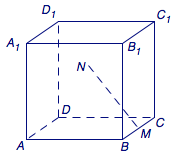
3、如图,在正方体\(ABCD-A_1B_1C_1D_1\)中,\(M\)为\(BC\)的中点,点\(N\)在四边形\(CDD_1C_1\)及其内部运动.若\(MN\perp A_1C_1\),则\(N\)点的轨迹为( )
A.线段
B.圆的一部分
C.椭圆的一部分
D.双曲线的一部分
4、当\(x\in [-2,1]\)时,不等式\(ax^3-x^2+4x+3\geqslant 0\)恒成立,则实数\(a\)的取值范围是_______.
5、已知函数\(f(x)=a_1\cos^2x+\left(a_2-1\right)\sin x\cos x+3\sin^2x\)(\(a_1^2+a_2^2\neq 0\))的图象是一条直线,则\(a_1+a_2=\)_______.
6、过边长为\(2\)的正方形中心作直线\(l\),将正方形沿直线\(l\)翻折,则翻折后的图形面积的最大值为_______.
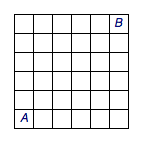
7、对于一个\(n\times n\)的正方形盒子,从\(A\)走到\(B\),每一步走一格,可以向左、向右、向上,但不能向下,且一次路径不能重复走同一个格子,则从\(A\)到\(B\)的不同走法数有_______.