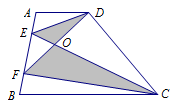
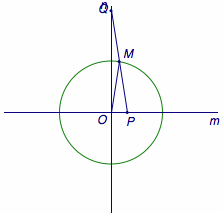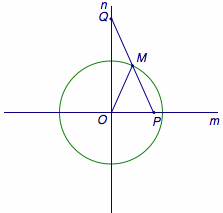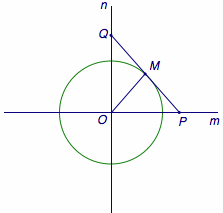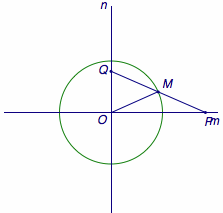
如图,梯形\(ABCD\)中,点\(E,F\)在腰\( AB\)上,\(AE=BF\),\(CE,DF\)相交于点\(O\),若梯形\(ABCD\)的面积为\(25\),\(\triangle OCD\)的面积为\(8\),则图中阴影部分的面积为_____.
2025年 12月 一 二 三 四 五 六 日 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 标签
-
近期文章
2025年 12月 一 二 三 四 五 六 日 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 标签