已知$a,b,c\geqslant 0$且$a+b+c=3$,求$m=a^2b^2+b^2c^2+c^2a^2$的最大值.
每日一题[997]用解析办法解平几问题
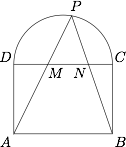
已知矩形$ABCD$中$AB=\sqrt 2BC$,以$CD$为直径向矩形外作半圆,设$P$为半圆上任意一点,直线$PA,PB$分别与$CD$相交于点$M,N$,求证:$CD^2=CM^2+DN^2$.
每日一题[995]分分合合
已知$a,b,c,d>0$,求证:$\dfrac{1}{a(a+b)}+\dfrac{1}{b(b+c)}+\dfrac{1}{c(c+d)}+\dfrac{1}{d(d+a)}\geqslant \dfrac{4}{ac+bd}$.
继续阅读
每日一题[994]分式函数的最值
已知$A$在线段$BC$上(不包含端点),$O$是直线$BC$外一点,且$\overrightarrow{OA}-2a\overrightarrow{OB}-b\overrightarrow{OC}=\overrightarrow 0$,则$\dfrac{a}{a+2b}+\dfrac{2b}{1+b}$的最小值是________.
每日一题[993]构造与论证
设$a,d$是正整数,求证:等差数列$\{a+nd\}$($n\in\mathbb N$)中有无穷多项,它们有相同的质因数.
每日一题[992]螺旋数学归纳法
求证:$\displaystyle \sum_{k=0}^{\left[\frac n2\right]}(-1)^k{\rm C}_{n-k}^k(2\cos x)^{n-2k}=\dfrac{\sin (n+1)x}{\sin x}$.
每日一题[991]左右不逢源
在$1,2,3,4,5,6,7,8,9,10,11,12,13$共$13$个数中挑出$k$个数,使得这$k$个数中任意两个的差都不是$5$和$8$,则$k$的最大值是_______.
每日一题[990]根与系数
已知$a,b,c$为正整数,方程$ax^2+bx+c=0$的两个实根$x_1,x_2$满足$-1< x_1<x_2< 1$,求$a+b+c$的最小值.
每日一题[989]层层转化求最值
已知$a,b,c,d\geqslant 0$且$a+b+c+d=4$,求$m=\dfrac{a}{b^3+4}+\dfrac{b}{c^3+4}+\dfrac{c}{d^3+4}+\dfrac{d}{a^3+4}$的最大值与最小值.
