每日一题[705]三次函数的性质

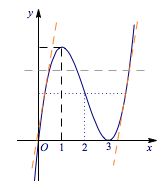
设关于$x$的方程$x(x-3)^2=m$有三个不同的实数解$a,b,c$，且$a<b<c$，则下列命题正确的是________．
(1) $abc$的取值范围是$(0,4)$；
(2) $a^2+b^2+c^2$为定值；
(3) $c-a$有最小值，没有最大值．

---

分析与解　(1)(2)．

(1) 由于函数$f(x)=x(x-3)^2$的极大值为$f(1)=4$，极小值为$f(3)=0$，于是$m$的取值范围是$(0,4)$．原方程即$x^3-6x^2+9x-m=0$，于是根据三次方程的韦达定理，有

$$\begin{cases} a+b+c=6,\\ ab+bc+ca=9,\\ abc=m,\end{cases}$$ 因此$abc$的取值范围即$m$的取值范围，为$(0,4)$．

(2) $a^2+b^2+c^2=(a+b+c)^2-2(ab+bc+ca)=18$为定值．

(3) 易得$1<b<3$，而$a+c=6-b$，$ac=9-b(6-b)=b^2-6b+9$，于是

$$\begin{split} c-a&=\sqrt{(a+c)^2-4ac}\\&=\sqrt{(6-b)^2-4(b^2-6b+9)}\\&=\sqrt{-3b^2+12b},\end{split}$$ 于是$c-a$的取值范围是$\left(3,2\sqrt 3\right]$，因此$c-a$没有最小值，有最大值．

注　可以结合下图去感受一下$c-a$的最值：

更多三次函数相关的内容见三次函数的性质．