这是2013年昌平区二模的压轴题：
如果函数\(y=f(x)\)的定义域为\(\bf R\)，对于定义域内的任意\(x\)，存在实数\(a\)使得\(f(x+a)=f(-x)\)成立，则称此函数具有“\(P(a)\)性质”．
(1) 判断函数\(y=\sin x\)是否具有“\(P(a)\)性质”，若具有“\(P(a)\)性质”，求出所有的\(a\)的值；若不具有“\(P(a)\)性质”，请说明理由；
(2) 设函数\(y=g(x)\)具有“\(P(\pm 1)\)性质”，且当\(-\dfrac 12\leqslant x \leqslant \dfrac 12\)时，\(g(x)=|x|\)．若\(y=g(x)\)与\(y=mx\)的交点个数为\(2013\)，求\(m\)的值．
2014年高考四川卷理科数学第21题、文科数学第21题（压轴题）：
已知函数 \(f(x)={\rm e}^x-ax^2-bx-1\)，其中\(a,b\in \bf R\)，\({\rm e}=2.71828\cdots\)为自然对数的底．
（1）设\(g(x)\)是函数\(f(x)\)的导函数，求函数\(g(x)\)在区间\([0,1]\)上的最小值；
（2）若\(f(1)=0\)，函数\(f(x)\)在区间\((0,1)\)内有零点，求\(a\)的取值范围．
已知\(\vec a,\vec b,\vec c\)两两均不共线，\(\vec a + \vec b \parallel \vec c\)，\(\vec b +\vec c\parallel \vec a\)，求证：\(\vec a+\vec b+\vec c=\vec 0\)．
2014年高考新课标II卷理科数学第21题（压轴题）：
已知函数\(f(x)={\rm e}^x-{\rm e}^{-x}-2x\)．
（1）讨论\(f(x)\)的单调性；
（2）设\(g(x)=f(2x)-4bf(x)\)，当\(x>0\)时，\(g(x)>0\)，求\(b\)的最大值；
（3）已知\(1.4142<\sqrt 2<1.4143\)，估计\(\ln 2\)的近似值（精确到\(0.001\)）．
已知\(x\in \left(0,\dfrac \pi 2\right)\)，求证：\(\sin {\sqrt x}<\sqrt {\sin x}\)．
一、填空题（本题共5小题，每小题8分，共40分）
1、设\(f(x)=\dfrac{x}{\sqrt{1+x^2}}\)，则\(n\)重复合函数\(f_n(x)=f(f(\cdots f(x)\cdots))=\)_______．
2、设多项式\(p(x)\)满足\(p\left(x^2+1\right)=\left(p(x)\right)^2+1\)和\(p(0)=0\)，则\(p(x)=\)_______.
3、设\(S_n=\sum\limits_{k=1}^n\dfrac{6^k}{\left(3^{k+1}-2^{k+1}\right)\left(3^k-2^k\right)}\)，则极限\(\lim\limits_{n\to\infty}S_n=\)_______.
4、对\(x>0\)，函数\(f(x)=\dfrac{\left(x+\dfrac1x\right)^6-\left(x^6+\dfrac1{x^6}\right)-2}{\left(x+\dfrac1x\right)^3+\left(x^3+\dfrac1{x^3}\right)}\)的最小值为_______．
5、假设\(20\)名学生中的每一名学生可从提供的六门课程中选学一门至六门，也可以一门都不选．试判断下列命题是否正确：存在\(5\)名学生和两门课程，使得这\(5\)名学生都选了这两门课，或者都没选，选填“正确”或“否”_______．
二、（本题共14分）
1、若\(a\)为正整数而\(\sqrt a\)不为整数，证明：\(\sqrt a\)为无理数.
2、试证：除\(0,0,0\)外，没有其他整数\(m,n,p\)使得\[m+n\sqrt2+p\sqrt3=0.\] 三、（本题共16分） 设\(a,b,c\)为三角形三边之长，\(p=\dfrac{a+b+c}2\),\(r\)为内切圆半径，证明：\[\dfrac1{(p-a)^2}+\dfrac1{(p-b)^2}+\dfrac1{(p-c)^2}\geqslant\dfrac1{r^2}.\]
四、（本题共12分） 证明：设\(m\)是任一正整数，则\(a_m=\dfrac12+\dfrac13+\dfrac14+\dfrac15+\cdots+\dfrac1{2^m}\)不是整数．
五、（本题共18分） 下图是2013年恒大足球俱乐部策划的主场与首尔FC足球队的亚冠决赛海报，左边是恒大队，右边是首尔队，该海报的寓意是什么？要求简单推导海报中两个数学式子的结果．一个数学式子是\(\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+\cdots}}}}\)(拉马努金式子)，另一个是\(\mathrm e^{\pi \mathrm i}+1\)(已知欧拉公式\(\mathrm e^{\pi \mathrm i}=\cos\alpha+\mathrm i\sin\alpha\))． 
一、填空题
1、\(\dfrac{x}{\sqrt{1+nx^2}}\)．
2、\(x\) 提示 方程\(p(x)-x=0\)有无数个零点，于是\(p(x)=x\)．
3、\(2\) 提示 裂项为\(\dfrac{2^k}{3^k-2^k}-\dfrac{2^{k+1}}{3^{k+1}-2^{k+1}}\)．
4、\(6\) 提示 函数\(f(x)=3\left(x+\dfrac 1x\right)\)．
5、否 提示 \(6\)门课中选\(3\)门共有\({\rm C}_6^3=20\)种不同的组合，让每个同学分别选一种组合，那么任何两门课同时选和同时不选的同学数均为\(4\)．
二、略
提示 均用反证法．
三、略
提示 \(pr=S\)，而\(S=\sqrt{p(p-a)(p-b)(p-c)}\)．
四、略
提示 设右边的公分母为\[\left[2,3,4,\cdots,2^m\right]=2^m\cdot p,\]其中\(p\)是一个奇数，两边同时乘以公分母，则左边是偶数，而右边为奇数．
注一 利用这个方法可以证明\(\sum\limits_{i=1}^n{\dfrac 1i}\)，其中\(n\in\mathcal N^*\)且\(n\geqslant 2\)均不是整数．另外，这个方法中从\(2\)的方幂出发也不是必须的．
注二 也可以两边同时乘以\(\dfrac{[2,3,\cdots,2^m]}p\)，其中\(p\)为右边各分母分解质因数后的最大奇素数因子，根据伯特兰-切比雪夫定理，含\(p\)的项唯一，进而即得．
五、\(3:0\)
提示 拉马努金恒等式，注意到\[n=\sqrt{1+(n-1)(n+1)},\]于是\[\begin{split}3&=\sqrt{1+2\cdot 4}\\&=\sqrt{1+2\sqrt{1+3\cdot 5}}\\&=\sqrt{1+2\sqrt{1+3\sqrt{1+4\cdot 6}}}\\&=\cdots\end{split}.\]
1、已知函数$f(x)=\ln x-2x$．
（1）求函数$f(x)$的单调区间；
（2）若两个不相等的正实数$x_1,x_2$满足$f(x_1)=f(x_2)$，证明：$x_1+x_2>1$．
注 以下试题均为学生回忆的试题，不能保证真实性和正确性．欢迎读者给出解答，谢谢！
1、函数\(y=\cos\left(\pi x\right),x\in (2013,2014]\)的反函数为_______．
2、如图为某空间几何体的展开图，则该空间几何体共有_______条棱．
3、除\(x=1\)外，圆\(x^2+y^2=1\)与圆\((x-2)^2+(y-3)^2=1\)的另一条公切线方程为_______．
4、散点\((1.0,0.9)\)，\((2.0,1.9)\)，\((3.0,3.2)\)对应的回归直线方程为_______．
5、\(y=\sin\left(\omega x+\varphi\right)\)与\(y=\sin\left(2x+\dfrac{\pi}{3}\right)\)的图象关于\(x=-1\)对称，则所有可能的\(\varphi=\)_______．
6、向量\((1,2)\)绕点\((1,1)\)顺时针旋转\(45^\circ\)后所得的向量为_______．
7、\(\left|2x-y\right|+\left|x-2y\right|\leqslant 3\)所表示的平面区域面积为_______．
8、离散型随机变量\(X\)满足：\(E(X)=1\)，\(D(X)=2\)，则\(E\left(X^2\right)=\)_______．
9、圆\(C:x^2+y^2-2x-2y+1=0\)内位于直线\(l:y=x\tan\theta\)下方的面积为\(S\)，其中\(\theta\in\left(0,\dfrac{\pi}{2}\right)\)．
（1）求\(S(\theta)\)的表达式；
（2）求函数\(S(\theta)\)与函数\(S'(\theta)\)的单调性；
（3）画出\(S(\theta)\)的草图．
10、证明椭圆的光学性质．
11、已知甲袋中装有\(5\)个红球，乙袋中装有\(5\)个白球．每次从甲、乙两袋中分别随机摸一个球，同时放入对方袋中．\(n\)次操作后，甲袋中红球的个数记为\(X\)．求\(X\)的分布列和数学期望．
说明 文科考生做前5题，理科考生做后5题，每题20分， 共100分．
1、设关于\(x\)的方程\(x^2-ax+2a-2=0\)在区间\(\left[0,\dfrac 32\right]\)内有根，求实数\(a\)的取值范围．
2、设\(a,b,c\)满足\(a+b+c=a^3+b^3+c^3=0\)，\(n\)为任意自然数，求\(a^{2n+1}+b^{2n+1}+c^{2n+1}\)的值．
3、证明：若\(n\)为不小于\(2\)的自然数，\(t\)为实数且\(\sin\dfrac{t}{2}\neq 0\)，则\[\sum_{k=1}^n\left(1+\sum_{p=1}^{k-1}2\cos pt\right)=\left(\dfrac{\sin\frac{nt}2}{\sin\frac t2}\right)^2.\]
4、一个等腰梯形的腰和底的长分别为\(\sqrt 2\)和\(3\)，求这个梯形面积的最大值．
5、求出所有实数\(x\)，使得\(\dfrac{x^2+4x-1}{7x^2-6x-5}\)与\(\dfrac{1-x}{1+x}\)同时为整数．
6、顶点为\(A\)的等腰三角形\(ABC\)的角\(B\)的平分线交\(AC\)于\(D\)，已知\(BC=BD+AD\)，求角\(A\)的度数．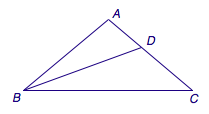 
7、设\(a,b,c\)是实数，方程\(x^3+ax^2+bx+c=0\)有\(3\)个正根，证明\(2a^3+9c\leqslant 7ab\)，并且等号成立当且仅当这\(3\)个正根相等． 继续阅读
