今天要吐槽的是2015年北京市东城区高三二模数学理科的第18题：
已知函数\(f(x)=x+a\cdot {\mathrm e}^{-x}\)．
（1）当\(a={\mathrm e}^2\)时，求函数\(f(x)\)在区间\([1,3]\)上的最小值；
（2）求证：存在实数\(x_0\in [-3,3]\)，有\(f(x_0)>a\)．
如图，已知正方形\(ABCD\)的边长为\(2\)，点\(E\)为\(AB\)的中点．以\(A\)为圆心，\(AE\)为半径，作弧交\(AD\)于点\(F\)．若\(P\)为劣弧\(EF\)上的动点，则\(\overrightarrow{PC}\cdot\overrightarrow{PD}\)的最小值为_______．
已知数列\(\left\{x_n\right\}\)满足\(\lim\limits_{n\to \infty}\left(x_n-x_{n-2}\right)=0\)，求证：\(\lim\limits_{n\to\infty}\dfrac{x_n-x_{n-1}}{n}=0\)．
证明：设\(y_n=x_n-x_{n-1}\)，\(n\in \mathcal N^*\)，则原问题转化为已知\(\lim\limits_{n\to \infty}\left(y_n+y_{n-1}\right)=0\)，求证：\(\lim\limits_{n\to\infty}\dfrac{y_n}{n}=0\)．
根据已知，有\(\forall \varepsilon>0\)，\(\exists N(\varepsilon)\in\mathcal N^*\)，使得当\(n>N\)时，均有\[\left|y_n+y_{n-1}\right|<\dfrac 12\varepsilon,\]此时有\[y_n=\left(y_n+y_{n-1}\right)+(-1)\left(y_{n-1}+y_{n-2}\right)+(-1)^2\left(y_{n-2}+y_{n-3}\right)+\cdots+(-1)^{n-N-1}\left(y_{N+1}+y_{N}\right)+(-1)^{n-N}y_N,\]从而\[\left|y_n\right|\leqslant \dfrac 12(n-N)\varepsilon+\left|y_N\right|,\]从而\[\dfrac{\left|y_n\right|}{n}\leqslant \dfrac 12\varepsilon -\dfrac{N}{2n}\varepsilon+\dfrac{\left|y_N\right|}{n}<\dfrac 12\varepsilon +\dfrac{\left|y_N\right|}{n},\]此时只需要取\(N_0=\max\left\{N(\varepsilon,\left[\dfrac{2\left|y_N\right|}{\varepsilon}\right]+1\right\}\)即可使得\[\dfrac{\left|y_n\right|}{n}<\varepsilon,\]因此\[\lim_{n\to\infty}\dfrac{\left|y_n\right|}{n}=0,\]进而原命题得证．
今天的题目是2015年北京市西城区高三二模数学理科的压轴题：
无穷数列\(P:a_1,a_2,\cdots,a_n,\cdots,\)满足\(a_i\in\mathcal N^*\)，且\(a_i\leqslant a_{i+1}\)（\(i\in\mathcal N^*\)）．对于数列\(P\)，记\(T_k(P)\)（\(k\in\mathcal N^*\)）表示集合\(\left\{n\left|a_n\geqslant k\right.\right\}\)中最小的数．
（1）若数列\(P:1,3,4,7,\cdots\)，写出\(T_1(P),T_2(P),\cdots,T_5(P)\)；
（2）若\(T_k(P)=2k-1\)，求数列\(P\)前\(n\)项的和；
（3）已知\(a_{20}=46\)，求\(\sum\limits_{i=1}^{20}{a_i}+\sum\limits_{j=1}^{46}{T_j(P)}\)的值．
已知非零向量\(\overrightarrow a\)和\(\overrightarrow b\)互相垂直，则\(\overrightarrow a+ \overrightarrow b\)和\(\overrightarrow a+2\overrightarrow b\)的夹角余弦值的最小值为_______．
已知\(x,y\in \mathcal R\)，\(\theta\in\left(\dfrac{\pi}4,\dfrac{\pi}2\right)\)，且满足\[\begin{cases}\dfrac{\sin\theta}{x}=\dfrac{\cos\theta}{y}\\\dfrac{\cos^2\theta}{x^2}+\dfrac{\sin^2\theta}{y^2}=\dfrac{10}{3\left(x^2+y^2\right)}\end{cases}\]求\(\dfrac{x}{y}\)的值．
已知函数\[f(x)=1+x-\dfrac{x^2}2+\dfrac{x^3}3-\dfrac{x^4}4+\cdots-\dfrac{x^{2014}}{2014}+\dfrac{x^{2015}}{2015},\]若函数\(f(x)\)的零点都在区间\([a,b]\)（其中\(a<b\)且\(a,b\in\mathcal Z\)）内，则\(b-a\)的最小值为_______．
抛物线的三条切线所围成的三角形称为切线三角形，对应的三个切点形成的三角形称为切点三角形，它们有很多美妙的性质．
1、切线三角形的外接圆过抛物线的焦点．
设抛物线的方程为\(E:x^2=2py\)，\(A\left(2pa,2pa^2\right)\)，\(B\left(2pb,2pb^2\right)\)，\(C\left(2pc,2pc^2\right)\)，则三条切线的方程分别为\[\begin{split}B'C'&:2ax-y-2pa^2=0,\\C'A'&:2bx-y-2pb^2=0,\\A'B'&:2cx-y-2pc^2=0,\end{split}\]进而可联立解得\[A'\left(p(b+c),2pbc\right),B'\left(p(c+a),2pca\right),C'\left(p(a+b),2pab\right).\]
因此，三角形\(A'B'C'\)外接二次曲线的方程为\[L_AL_B+\lambda L_BL_C+\mu L_CL_A=0,\]其中\(L_A\)、\(L_B\)、\(L_C\)分别为\(A\)、\(B\)、\(C\)处切线方程的左侧代数式．将其整理为\[Ax^2+By^2+Cxy+Dx+Ey+F=0\]的形式，其中\[\begin{split}A&=4(ab+\lambda bc+\mu ca),\\B&=1+\lambda+\mu,\\C&=-2\left[(a+b)+\lambda (b+c)+\mu (c+a)\right],\end{split}\]为了使得该方程表示圆，有\[A=B\land B=0,\]从而解得\[\begin{cases}\lambda=\dfrac{\left(1+4a^2\right)\left(b-c\right)}{\left(1+4c^2\right)\left(a-b\right)},\\\mu=\dfrac{\left(1+4b^2\right)\left(c-a\right)}{\left(1+4c^2\right)\left(a-b\right)},\end{cases}\]于是三角形\(A'B'C'\)外接圆的方程为\[\sum_{cyc}\left[\left(1+4c^2\right)\left(a-b\right)\left(2ax-2pa^2\right)\left(2bx-y-2pb^2\right)\right]=0,\]将抛物线的焦点坐标\(F\left(0,\dfrac{p}{2}\right)\)代入左边，有\[\begin{split}&\quad \sum_{cyc}\left[\left(1+4c^2\right)\left(a-b\right)\left(-\dfrac p2-2pa^2\right)\left(-\dfrac p2-2pb^2\right)\right]\\&=\dfrac{p^2}{4}\left(1+4a^2\right)\left(1+4b^2\right)\left(1+4c^2\right)\sum_{cyc}\left(a-b\right)\\&=0,\end{split}\]因此性质1得证．
2、切线三角形的垂心在抛物线的准线上．
根据之前的结果，有\[\begin{split}A'H&:y-2pbc=-\dfrac{1}{2a}\left[x-p(b+c)\right],\\B'H&:y-2pca=-\dfrac{1}{2b}\left[x-p(c+a)\right],\end{split}\]从而可得垂心\(H\)的纵坐标满足\[2a(y-2pbc)-2b(y-2pca)=p(b+c)-p(c+a),\]即\[y=-\dfrac{p}{2},\]因此性质2得证．
3、切线三角形的面积是切点三角形面积的一半．
根据之前的结果，有\[\begin{split}S_{\triangle ABC}&=\dfrac 12\begin{vmatrix}1&1&1\\2pa&2pb&2pc\\2pa^2&2pb^2&2pc^2\end{vmatrix}\\&=2p^2\left|(a-b)(b-c)(c-a)\right|,\end{split}\]而\[\begin{split}S_{\triangle A'B'C'}&=\dfrac 12\begin{vmatrix}1&1&1\\p(b+c)&p(c+a)&p(a+b)\\2pbc&2pca&2pab\end{vmatrix}\\&=p^2\left|(a-b)(b-c)(c-a)\right|,\end{split}\]因此性质3得证．
4、抛物线的焦点到切线三角形三个顶点的距离之积与到切点三角形三个顶点的距离之积相等．
根据之前的结果，有\[\begin{split}FA^2\cdot FB^2\cdot FC^2&=\prod_{cyc}\left[\left(2pa\right)^2+\left(\dfrac{p}{2}-2pa^2\right)^2\right]\\&=p^2\prod_{cyc}\left(2a^2+\dfrac{1}{2}\right)^2,\end{split}\]而\[\begin{split}FA'^2\cdot FB'^2\cdot FC'^2&=\prod_{cyc}\left[\left(p(b+c)\right)^2+\left(\dfrac{p}{2}-2pbc\right)^2\right]\\&=p^2\prod_{cyc}\left[\left(2b^2+\dfrac 12\right)\left(2c^2+\dfrac 12\right)\right],\end{split}\]因此性质4得证．
5、对切点三角形而言，可以视切线三角形为割线应用“Menelaus定理”．
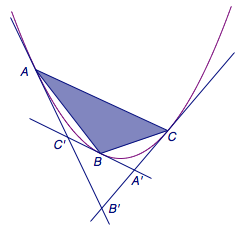即在图中有\(\dfrac{AB'}{B'C}\cdot\dfrac{CA'}{B'B}\cdot\dfrac{BC'}{C'A}=1\)．
先证明
引理 过点\(P(x_0,y_0)\)作二次曲线\[Ax^2+By^2+Dx+Ey+F=0\]的割线\(PMN:y=kx+m\)，其中\(M\)、\(N\)在二次曲线上，那么\[PM\cdot PN=\left(1+k^2\right)\cdot\left|\dfrac{Ax_0^2+By_0^2+Dx_0+Ey_0+F}{A+Bk^2}\right|.\]
从而可以得到切线长的计算公式，进而可以推得更一般的结论（对一般圆锥曲线均成立），此处从略．
如图所示，在三角形\(ABC\)和三角形\(AEF\)中，\(B\)是\(EF\)的中点，\(AB=EF=1\)，\(BC=6\)，\(CA=\sqrt{33}\)，若\(\overrightarrow{AB}\cdot \overrightarrow{AE}+\overrightarrow {AC}\cdot \overrightarrow{AF}=2\)，则\(\overrightarrow{EF}\)与\(\overrightarrow{BC}\)夹角的余弦值为_______．
