在角含半角模型之90°含45°（一）中我们知道当\(\angle EBF=45^\circ\)时，\(EB\)平分\(\angle AEF\)；反之，若$EB$平分$\angle AEF$，则$\angle EBF=45^\circ$．证明如下图．作\(BH\perp EF\)，则\(BH=BA=BC\)，从而得证．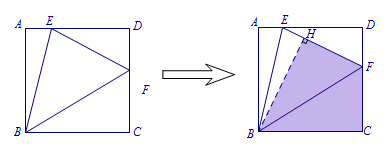
接下来我们看看这一结论的应用．
例题 正方形\(ABCD\)中，\(M\)为边\(AD\)上一动点（不与\(A、D\)重合），作等腰梯形\(BMNC\)，其中\(BM\parallel CN\)，\(BC=MN\)，\(AB=1\)，\(AM=x\)，\(CP=y\)，求\(y\)关于\(x\)的函数关系式．
继续阅读
2015年北京市海淀区高三期中理科数学第20题（压轴题）：
已知$x$为实数，用$[x]$表示不超过$x$的最大整数，例如$[1.2]=1$，$[-1.2]=-2$，$[1]=1$．
对于函数$f(x)$，若存在$m\in\mathcal R\land m\notin\mathcal Z$，使得$f(m)=f([m])$，则称函数$f(x)$是$\Omega$函数．
（1）判断函数$f(x)=x^2-\dfrac 13x$，$g(x)=\sin\pi x$是否是$\Omega$函数；（只需写出结论）
（2）设函数$f(x)$是定义在$\mathcal R$上的周期函数，其最小正周期是$T$，若$f(x)$不是$\Omega$函数，求$T$的最小值；
（3）若函数$f(x)=x+\dfrac ax$是$\Omega$函数，求$a$的取值范围．
这是我在QQ群中国数学解题研究会中看到的问题：
如图，在平面直角坐标系$xOy$中，圆$C_1:x^2+y^2=4$，圆$C_2:x^2+y^2=16$，点$M(1,0)$，动点$P$、$Q$分别在圆$C_1$和圆$C_2$上，满足$MP\perp MQ$，则线段$PQ$的取值范围是_______．
2015年北京市海淀区高三期中理科数学试题第14题：
对于数列$\{a_n\}$，若对任意$m,n\in\mathcal N^*\land m\neq n$，都有$\dfrac{a_m-a_n}{m-n}\geqslant t$（$t$为常数）成立，则称数列$\{a_n\}$具有性质$P(t)$．
（1）若数列$\{a_n\}$的通项公式为$a_n=2^n$，且具有性质$P(t)$，则$t$的最大值为_______；
（2）若数列$\{a_n\}$的通项公式为$a_n=n^2-\dfrac an$，且具有性质$P(10)$，则实数$a$的取值范围是_______．
卡特兰（Catalan）数来源于卡特兰解决凸$n+2$边形的剖分时得到的数列$C_n$，在数学竞赛、信息学竞赛、组合数学、计算机编程等方面都会有其不同侧面的介绍．卡特兰问题的解决过程应用了大量的映射方法，堪称计数的映射方法的典范．为了便于读者理解，我们先介绍一些卡特兰问题的简单变形，再介绍卡特兰问题及其解法．
函数的零点问题常见的处理思路有两种，一种思路是将一个函数的零点问题转化成两个（较简单的）函数的交点问题，再结合图象进行判断，需要注意的是函数本身可以进行适当的代数变形以使得转化成的两个函数的草图更容易作出；另一种思路是将这个函数作为整体进行考虑，借助这个函数的性质直接得到结果，有时函数的性质需要借助导数去研究．
2014年湖南高考理科第10题（选择压轴题）：
已知函数\(f(x)=x^2+{\mathrm e}^x-\dfrac 12,x<0\)与\(g(x)=x^2+\ln(x+a)\)的图象上存在关于\(y\)轴对称的点，则\(a\)的取值范围是_______．
对于两个有限集合$M$、$N$，如果我们能够建立单射$f:M \to N$，那么${\rm{card}}(N)$（其中${\rm{card}}$表示有限集合中元素的数目）．进一步，如果我们能够证明$f$是满射，那么就可以得到${\rm{card}}(M )={\rm{card}}(N)$．这一简单结论在组合计数中应用很广泛，举例如下．
已知$\{a_n\}$是等差数列，$S_n$为其前$n$项和．若正整数$i,j,k,l$满足$i\leqslant k \leqslant l \leqslant j$，且$i+j=k+l$，则（ ）
A．$a_ia_j\leqslant a_ka_l$
B．$a_ia_j\geqslant a_ka_l$
C．$S_iS_j\leqslant S_kS_l$
D．$S_iS_j\geqslant S_kS_l$
