Math173

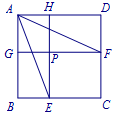
定义区间$(a,b)$，$[a,b)$，$(a,b]$，$[a,b]$的长度均为$d=b-a$，多个区间并集的长度为各区间长度之和，例如$(1,2)\cup [3,5)$的长度$d=(2-1)+(5-3)=3$．设$f(x)=[x]\cdot \{x\}$，$g(x)=x-1$，其中$[x]$表示不超过$x$的最大整数，$\{x\}=x-[x]$．若用$d_1$、$d_2$、$d_3$分别表示不等式$f(x)>g(x)$、方程$f(x)=g(x)$、不等式$f(x)<g(x)$解集区间的长度，则当$-2016\leqslant x\leqslant 2016$时，$d_1=$____；$d_2=$____；$d_3=$____．

继续阅读 →

已知满足条件$x^2+y^2\leqslant 1$的点$(x,y)$构成的平面区域的面积为$S_1$，满足条件$[x]^2+[y]^2\leqslant 1$的点$(x,y)$构成的平面区域的面积为$S_2$（其中$[x],[y]$分别表示不超过$x,y$的最大整数），则$S_1$与$S_2$的大小关系是______．

继续阅读 →

2015年高考数学湖北文科第17题（填空压轴题）：

$a$为实数，函数$f\left(x\right)={\left|{x^2-ax}\right|}$在区间$\left[0,1\right]$上的最大值记为$g\left(a\right)$．当$a=$_____时，$g\left(a\right)$的值最小．

继续阅读 →

设函数$f(x)$在$\mathcal{R}$上存在导数$f'(x)$，对任意$x\in\mathcal{R}$，有$f(-x)+f(x)=x^2$，且在$(0,+\infty)$上$f'(x)>x$．若$f(2-a)-f(a)\geqslant 2-2a$，则实数$a$的取值范围为_____．

继续阅读 →

2015高考数学湖北文科第10题（选择压轴题）：

已知集合$A=\left\{\left(x,y\right) \left|\right. x^2+y^2\leqslant 1,x,y\in{\mathcal{Z}}\right\}$，$B=\left\{(x,y) \big||x|\leqslant 2,|y|\leqslant 2,x,y\in{\mathcal{Z}}\right\}$，定义集合$A\oplus B=\left\{\left(x_1+x_2,y_1+y_2\right) \left|\right. \left(x_1,y_1\right)\in A,\left(x_2,y_2\right)\in B\right\}$，则$A\oplus B$中元素的个数为____．

继续阅读 →

2015高考数学广东文10（选择压轴题）：

若集合$E=\left\{\left(p,q,r,s\right) \left|\right. 0\leqslant p<s\leqslant 4,0\leqslant q<s\leqslant 4,0\leqslant r<s\leqslant 4\ \text{且} \ p,q,r,s\in {\mathcal{N}}\right\}$，$F=\left\{\left(t,u,v,w\right) \left|\right. 0\leqslant t<u\leqslant 4,0\leqslant v<w\leqslant 4\ \text{且} \ t,u,v,w\in {\mathcal{N}}\right\}$，用${\mathrm{card}}\left(X\right)$表示集合$X$中元素个数，则${\mathrm{card}}\left(E\right)+{\mathrm{card}}\left(F\right)=$____．

继续阅读 →

2015年高考数学重庆卷文科第22题（解答压轴题）：

如图，椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为$F_1$，$F_2$，过$F_2$的直线交椭圆于$P$，$Q$两点，且$PQ\perp PF_1$．若 ${\left|{PQ}\right|}=\lambda {\left|{PF_1}\right|}$，且$\dfrac 34\leqslant \lambda<\dfrac 43$，试确定椭圆离心率$e$的取值范围．

继续阅读 →