每日一题[204] “垂径定理”

2014年全国高中数学联赛山东省预赛第13题：

设点\(O\)为椭圆的中心，点\(A\)为椭圆上异于顶点的任意一点，过点\(A\)作长轴的垂线，垂足为\(M\)，连接\(AO\)并延长交椭圆于另一点\(B\)，连接\(BM\)并延长交椭圆于点\(C\)，问是否存在椭圆，使得\(BA\perp CA\)？

解    记\(A(m,n)\)，\(B(-m,-n)\)，\(M(m,0)\)，则根据椭圆的“垂径定理”，有\[k_{CA}\cdot k_{CB}=-\dfrac{b^2}{a^2},\]而\[k_{CA}=-\dfrac{1}{k_{AB}}=-\dfrac mn,\]且\[k_{CB}=k_{BM}=\dfrac{n}{2m},\]于是可得\[\left(-\dfrac mn\right)\cdot\dfrac{n}{2m}=-\dfrac{b^2}{a^2},\]化简得\[a^2=2b^2.\]

因此存在符合题意的椭圆使得\(BA\perp CA\)，只需椭圆的离心率为\(\dfrac{\sqrt 2}2\)即可．

注    2012年高考江苏卷第18题基本与本题一致：

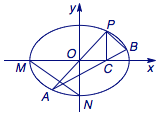
如图，在平面直角坐标系\(xOy\)中，\(M\)、\(N\)分别是椭圆\(\dfrac{x^2}{4}+\dfrac{y^2}2=1\)的顶点，过坐标原点的直线交椭圆于\(P\)、\(A\)零点，其中点\(P\)在第一象限，过\(P\)作\(x\)轴的垂线，垂足为\(C\)，连接\(AC\)，并延长交椭圆于点\(B\)，设直线\(PA\)的斜率为\(k\)．

（1）当\(PA\)平分线段\(MN\)时，求\(k\)的值；

（2）设\(k=2\)时，求点\(P\)到直线\(AB\)的距离\(d\)；

（3）对任意\(k>0\)，求证：\(PA\perp PB\)．