每日一题[1447]向量共线

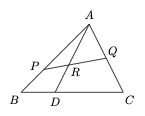
已知 $\triangle ABC$ 中，$D$ 为底边 $BC$ 上一点，且 $\dfrac{BD}{DC}=\lambda$，$P,Q$ 分别为 $AB,AC$ 上一点，$PQ$ 与 $AD$ 交于点 $R$，$\dfrac{AD}{AR}=\mu_0$，$\dfrac{AB}{AP}=\mu_1$，$\dfrac{AC}{AQ}=\mu_2$，求证：$\mu_0=\dfrac{\mu_1+\lambda\cdot \mu_2}{1+\lambda}$．

答案

解析 只需要证明

$$\dfrac{AR}{AD}\cdot \left(\dfrac{1}{1+\lambda}\cdot \dfrac{AB}{AP}+\dfrac{\lambda}{1+\lambda}\cdot \dfrac{AC}{AQ}\right)=1,$$ 即 $$\dfrac{AR}{AD}\cdot \left(\dfrac{DC}{BC}\cdot \dfrac{AB}{AP}+\dfrac{BD}{BC}\cdot \dfrac{AC}{AQ}\right)=1.$$ 考虑到 $$\begin{split}\overrightarrow {AR}&=\dfrac {AR}{AD}\overrightarrow{AD}\\ &=\dfrac{AR}{AD}\cdot \left(\dfrac{DC}{BC}\overrightarrow{AB}+\dfrac{BD}{BC}\overrightarrow{AC}\right)\\ &=\dfrac{AR}{AD}\cdot \left(\dfrac{DC}{BC}\cdot \dfrac{AB}{AP}\overrightarrow{AP}+\dfrac{BD}{BC}\cdot \dfrac{AC}{AQ}\overrightarrow{AQ}\right),\end{split}$$ 而 $P,R,Q$ 三点共线，于是命题得证．