今天的题目是2013年四川高考理科数学卷选择题的最后一题改成的填空题.
设函数\(f(x)=\sqrt{{\mathrm e}^x+x-a}\)(\(a\in\mathcal R\)).若曲线\(y=\sin x\)上存在点\((x_0,y_0)\)使得\(f(f(y_0))=y_0\),则\(a\)的取值范围是_________.
对于函数\(y=f(x)\),方程\(f(x)=x\)的根称为函数\(f(x)\)的(一阶)不动点;方程\(f(f(x))=x\)的根称为函数\(f(x)\)的二阶不动点.当然,我们也可以以此类推定义\(n\)阶不动点.有以下引理:
方程\(f\left(f(x)\right)=x\)的解为曲线\(y=f(x)\)与曲线\(x=f(y)\)(这两条曲线关于直线\(y=x\)对称)的交点的横坐标.
回到本题,根据引理,不难求得,\(a\)的取值范围是\([1,{\mathrm e}]\).如图.
点评 这是处理\(f(f(x))=x\)的常用方法.下面给出两道自主招生题作为练习.
1、(2008年上海交大)已知函数\(f(x)=ax^2+bx+c(a\neq 0)\),且\(f(x)=x\)没有实数根.问:\(f(f(x))=x\)是否有实数根?请证明你的结论.
2、(2009年上海交大)证明:若\(f(f(x))\)有唯一不动点,则\(f(x)\)也有唯一不动点.
2015年3月22日补充
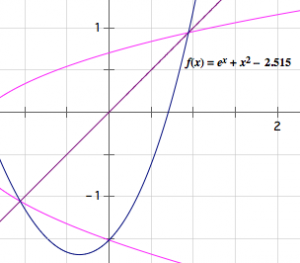
易错题 已知函数\(f(x)={\rm e}^x+x^2-a\),方程\(f\left(f(x)\right)=x\)在区间\([0,1]\)上有且只有一个解,求\(a\)的取值范围.
练习题 已知函数\(f(x)=\left|x^2-ax\right|-2\),且函数\(y=f(x+2)\)是偶函数.
(1)求实数\(a\)的值;
(2)设函数\(y=g(x)\),集合\(M=\left\{x\left|g(x)-x=0\right.\right\}\),\(N=\left\{x\left|g\left(g(x)\right)-x=0\right.\right\}\).
① 证明:\(M\subseteq N\);
② 如果\(g(x)=f\left(\left|x\right|\right)\),集合\(P=\left\{x\left|g\left(g(x)\right)-x=0\land \left|\right.x\left.\right|\leqslant 2\right.\right\}\),那么集合\(P\)中的元素个数为_______.
参考答案 (1)\(a=4\);(2)①略;②\(5\).



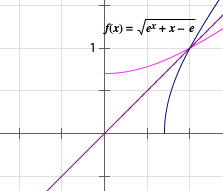
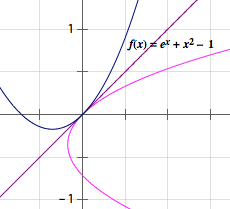
Pingback引用通告: 每日一题[853]函数的不动点 | 数海拾贝内容系统
Pingback引用通告: 每日一题[853]函数的不动点 | Math173
Pingback引用通告: 一类特殊函数的稳定点 | Math173
有点搞晕乎了,是不是说f(x)有几个不动点,就有几个二阶不动点?
二阶不动点可以比不动点个数多.