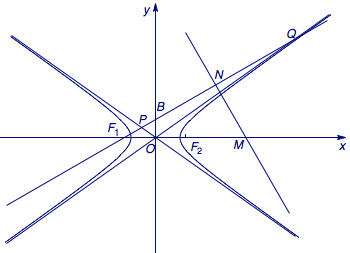
2012年高考浙江卷理科数学第8题:
如图,\(F_1\)、\(F_2\)分别是双曲线\(C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)(\(a>b>0\))的左、右焦点,\(B\)是虚轴的端点,直线\(F_1B\)与\(C\)的两条渐近线分别交于\(P\)、\(Q\)两点,线段\(PQ\)的垂直平分线与\(x\)轴交于点\(M\).若\(MF_2=F_1F_2\),则\(C\)的离心率为_______.
正确答案是\(\dfrac{\sqrt 6}2\).
解 根据题意,设\(F_1(-c,0)\),则\(M(3c,0)\).直线\(PQ\)的斜率为\[\frac{y_B-y_{F_1}}{x_B-x_{F_1}}=\frac bc,\]根据一般圆锥曲线的“垂径定理”,直线\(ON\)斜率满足\[k_{PQ}\cdot k_{ON}=\frac {b^2}{a^2},\]于是直线\(ON\)的斜率为\(\dfrac{bc}{a^2}\).另一方面,直线\(MN\)的斜率为\(-\dfrac cb\).因此设点\(N(x,y)\),则\[\begin{cases}\dfrac y{x+c}=\dfrac bc,\\\dfrac yx=\dfrac{bc}{a^2},\\\dfrac{y}{x-3c}=-\dfrac cb,\end{cases}\]从中消去\(x\)、\(y\)得\[\frac{a^2}{bc}-\frac{3b}{c}=-\frac bc,\]整理得\[3c^2=2a^2,\]从而离心率\[e=\frac{\sqrt 6}2.\]