三射线定理及其典型应用

三射线定理    如图，$PA$、$PB$、$PC$分别是从$P$出发的三条射线，$\angle APC$、$\angle BPC$、$\angle APB$分别为$\alpha$、$\beta$、$\theta$，二面角$A-PC-B$（记其大小为$\varphi$）满足：

$$\cos\theta=\cos\alpha\cdot\cos\beta+\sin\alpha\cdot\sin\beta\cdot\cos\varphi.$$

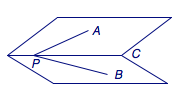
三射线定理描述了异面共边的两个角的另外两边构成的角（空间斜角）与这两个角形成的二面角（空间正角）之间的数量关系，因此往往用来求二面角的大小或者空间斜角的大小．三射线定理中的基本图形又称为三面角．

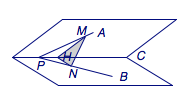
证明    如图，过射线$PC$上一点$H$作垂直于$PC$的平面，射线$PA$、$PB$分别与该平面相交于$M$、$N$两点．

方法一    利用空间向量

根据已知，有

$$\begin{split}\overrightarrow{PM}\cdot\overrightarrow{PN}&=\left(\overrightarrow{PH}+\overrightarrow{HM}\right)\cdot\left(\overrightarrow{PH}+\overrightarrow{HN}\right)\\&=PH^2+\overrightarrow{HM}\cdot\overrightarrow{HN}\\&=PH^2+HM\cdot HN\cdot\cos\varphi,\end{split}$$ 又 $$\overrightarrow{PM}\cdot\overrightarrow{PN}=PM\cdot PN\cos\theta,$$ 于是两边同除以$PM\cdot PN$得 $$\cos\theta=\cos\alpha\cdot\cos\beta+\sin\alpha\cdot\sin\beta\cdot\cos\varphi.$$

方法二    利用余弦定理

在三角形$MNP$和三角形$MNH$中分别应用余弦定理，有

$$\begin{split}MN^2&=MP^2+NP^2-2\cdot MP\cdot NP\cdot \cos \theta,\\MN^2&=MH^2+NH^2-2\cdot MH\cdot NH\cdot \cos \varphi,\end{split}$$ 两式相减得 $$0=2PH^2-2\cdot MP\cdot NP\cdot \cos\theta+2\cdot MH\cdot NH\cdot \cos\varphi,$$ 移项整理即得．

三射线定理的记忆    可以借助两角差的余弦公式记忆，当$\varphi=0,\pi$时，三射线定理退化为两角和与差的余弦公式．当$\varphi=\dfrac{\pi}2$时，三射线定理变成著名的三余弦定理：

$$\cos\theta=\cos\alpha\cdot\cos\beta.$$

接下来通过两道例题说明该定理在空间求角时的作用．

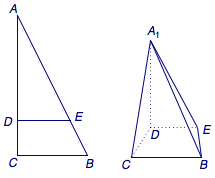
例1 （知斜求正）如图，在直角三角形$ABC$中，$C$为直角，$BC=3$，$AC=6$，$D$、$E$分别是$AC$、$AB$上的点，且$DE\parallel BC$，$DE=2$，将$\triangle ADE$沿$DE$折起到$\triangle A_1DE$的位置，使$A_1D\perp CD$．求平面$A_1CD$与平面$A_1BE$所成锐角的余弦值．

解    这是一道由2012年高考北京卷理科数学第16题改编的习题．

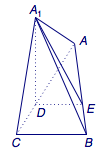
如图，在底面$BCDE$里分别延长$CD$和$BE$，交于$A$（实际上就是在未折叠的三角形$ABC$还原在直观图中），于是所求的锐角就是二面角$C-A_1A-B$的大小．

我们可以利用三面角$A-A_1DE$中解决问题．令$\angle A_1AD=\alpha$，$\angle EAA_1=\beta$，$\angle CAB=\theta$，$C-A_1A-B=\varphi$，而

$$\cos\alpha=\dfrac{\sqrt 2}2,\cos\beta=\dfrac{\sqrt 2}{\sqrt 5},\cos\theta=\dfrac{2}{\sqrt 5},$$ 于是 $$\dfrac{2}{\sqrt 5}=\dfrac{\sqrt 2}2\cdot\dfrac{\sqrt 2}{\sqrt 5}+\dfrac{\sqrt 2}2\cdot\dfrac{\sqrt 3}{\sqrt 5}\cdot\cos\varphi,$$ 解得 $$\cos\varphi=\dfrac{\sqrt 6}3.$$

事实上，取$A_1A$的中点$M$，则$\angle DME$即为二面角$C-A_1A-B$的平面角．

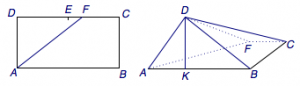
例2（知正求斜）如图，在长方形$ABCD$中，$AB=2$，$BC=1$，$E$为$DC$中点，$F$为线段$EC$（端点除外）上一动点．现将$\triangle AFD$沿$AF$折起，使平面$ABD$与平面$ABC$垂直．在平面$ABD$内过点$D$作$DK\perp AB$，$K$为垂足．设$AK=t$，则$t$的取值范围是_______．

解    这是2012年高考浙江卷理科数学第17题．

我们可以利用三面角$A-DKF$解决问题．令$\angle DAK=\alpha$，$\angle FAK=\beta$，$\angle DAF=\theta$，且$D-AK-F=\dfrac{\pi}2$，于是可得

$$\cos\angle DAF=\cos\angle DAK\cdot\cos\angle FAK,$$ 即 $$\dfrac{DA}{AF}=\dfrac{AK}{AD}\cdot\dfrac{DF}{AF},$$ 于是 $$AK=\dfrac{AD^2}{DF},$$ 其取值范围不难求得为$\left(\dfrac 12,1\right)$．

接下来给出两道练习题．

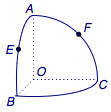
练习1、如图，$O$是半径为$1$的球的球心，点$A$、$B$、$C$在球面上，$OA$、$OB$、$OC$两两垂直，$E$、$F$分别是大圆弧$AB$与$AC$的中点，则点$E$、$F$在该球面上的球面距离是_______．

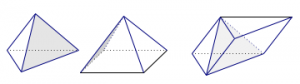
练习2、如图，一个正四面体和一个正四棱锥的所有棱长均为$1$，将正四面体与正四棱锥组合起来，使得正四面体的其中一个面与正四棱锥的一个侧面重合．问得到的多面体有多少个面？

练习3、(2016年全国2卷理科第19题)已知菱形$ABCD$的对角线$AC$与$BD$交于点$O$，$AB=5$，$AC=6$，点$E,F$分别在$AD,CD$上，$AE=CF=\dfrac 54$，$EF$交$BD$于点$H$．将$\triangle DEF$沿$EF$折到$\triangle D'EF$的位置，$OD'=\sqrt{10}$，求二面角$B-D'A-C$的正弦值．

参考答案

练习1、$\dfrac{\pi}3$

练习2、组合体为三棱柱，有$5$个面．

练习3、容易计算得$AO=3$，$BO=4$．由$AE=CF=\dfrac 54$可得

$$\dfrac{AE}{ED}=\dfrac{OH}{HD}=\dfrac{CF}{FD}=\dfrac 13,$$ 于是$OH=1$，$HD'=3$，进而$OD'=\sqrt{10}$，$CD'=\sqrt{19}$，$BD'=\sqrt{34}$．于是 $$\cos\angle BD'C=\cos\angle BD'A=\dfrac{34+19-25}{2\sqrt{34}\cdot\sqrt{19}}=\dfrac{14}{\sqrt{34}\cdot\sqrt{19}},$$ 而 $$\cos\angle CD'A=\dfrac{19+19-36}{2\cdot\sqrt{19}\cdot\sqrt{19}}=\dfrac{1}{19}.$$ 于是 $$\sin\angle BD'A=\dfrac{15\sqrt{2}}{\sqrt{34}\cdot\sqrt{19}},\sin\angle CD'A=\dfrac{6\sqrt{10}}{19},$$ 根据三面角定理，有 $$\dfrac{14}{\sqrt{34}\cdot\sqrt{19}}=\dfrac{14}{\sqrt{34}\cdot\sqrt{19}}\cdot\dfrac{1}{19}+\dfrac{15\sqrt{2}}{\sqrt{34}\cdot\sqrt{19}}\cdot\dfrac{6\sqrt{10}}{19}\cdot\cos\theta,$$ 其中$\theta=B-D'A-C$．易得$\cos\theta=\dfrac{7}{5\sqrt 5}$，于是$\sin\theta=\dfrac{2\sqrt{95}}{25}$．

---

更多的内容可以参考：

《每日一题[46] 三射线定理》

《每日一题[154] 折叠中的二面角》

《每日一题[202] 又见三射线》

《每日一题[255] 代表平面—出击！》