已知$A,B,C$是球$O$的球面上的三点,$\angle AOB=\angle AOC=45^\circ$,若三棱锥$O-ABC$体积的最大值为$\dfrac 23$,则球$O$的表面积为_______.
分析一 不难得知$\triangle AOB$与$\triangle AOC$全等,因此整个图形关于线段$BC$的垂直平分面对称.取$BC$的中点$M$,则$$V_{O-ABC}=\dfrac 13\cdot S_{\triangle OAM}\cdot BC,$$进而选择合适的参数展开计算.
解 设$\angle OAM=\alpha$,$\angle BAM=\beta$,$OA=OB=OC=r$,则根据三射线定理,有$$\cos\alpha\cdot \cos\beta=\cos\dfrac{3\pi}8,$$而\[\begin{split} V_{O-ABC}&=\dfrac 13\cdot S_{\triangle OAM}\cdot BC \\ &=\dfrac 16\sin\alpha\cdot AO\cdot AM\cdot BC \\ &=\dfrac 43r^3\cdot \cos^2\dfrac{3\pi}8\cdot \sin\alpha\cdot \cos\beta\cdot \sin\beta\\&=\dfrac 43r^3\cdot \cos^2\dfrac{3\pi}8\cdot\sqrt{(1-\cos^2\alpha)\cdot\cos^2\beta\cdot (1-\cos^2\beta)} \\ &=\dfrac 43r^3\cdot \cos^2\dfrac{3\pi}8\cdot\sqrt{\left(\cos^2\beta-\cos^2\dfrac{3\pi}8\right)(1-\cos^2\beta)}\\ &\leqslant \dfrac 43r^3\cdot \cos^2\dfrac{3\pi}8\cdot\dfrac{1-\cos^2\dfrac{3\pi}8}{2}\\ &=\dfrac {1}{12}r^3,\end{split}\]其中均值不等式的等号当$\cos 2\beta=\cos^2\dfrac{3\pi}8$时取得.因此不难得到$r=2$,于是球$O$的表面积为$16\pi$.
分析二 如图,根据题意,在变化的过程中,$\triangle AOB$和$\triangle AOC$保持不变,而它们的夹角发生变化,抓住运动中的不变量分析问题.
解 设$\angle BHC$为二面角$B-OA-C$的平面角,记为$\theta$,则$$V_{O-ABC}=\dfrac 13\cdot S_{\triangle BHC}\cdot OA=\dfrac 1{12}r^3\cdot\sin\theta,$$于是当平面$OAC$与平面$OAB$垂直时,三棱锥$O-ABC$的体积最大.因此不难得到$r=2$,于是球$O$的表面积为$16\pi$.


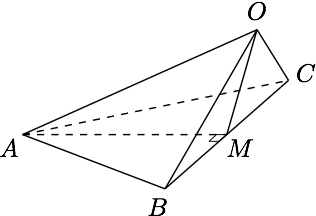
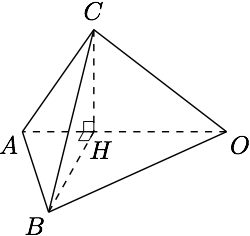
方法一中最大值为三分之二如何体现?
$\dfrac{1}{12}r^3=\dfrac 23$......