2014年高考四川卷理科数学第10题（选择压轴题）：
已知\(F\)为抛物线\(y^2=x\)的焦点，点\(A\)、\(B\)在该抛物线上且位于\(x\)轴的两侧，\(\overrightarrow{OA}\cdot\overrightarrow{OB}=2\)（其中\(O\)为坐标原点），则三角形\(ABO\)与三角形\(AFO\)的面积之和的最小值是（ ）
A．\(2\)
B．\(3\)
C．\(\dfrac{17\sqrt 2}8\)
D．\(\sqrt{10}\)
2014年高考湖南卷文科数学第10题（选择压轴题），理科数学第16题（填空压轴题）：
在平面直角坐标系中，\(O\)为原点，\(A(-1,0)\)，\(B(0,\sqrt 3)\)，\(C(3,0)\)，动点\(D\)满足\(\left|\overrightarrow{CD}\right|=1\)，则\(\left|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}\right|\)的取值范围是（ ）
A．\([4,6]\)
B．\(\left[\sqrt{19}-1,\sqrt{19}+1\right]\)
C．\(\left[2\sqrt 3,2\sqrt 7\right]\)
D．\(\left[\sqrt 7-1,\sqrt 7+1\right]\)
2014年高考福建卷文科数学第12题（原题为选择压轴题，有改动）：
在平面直角坐标系中，两点\(P_1(x_1,y_1)\)，\(P_2(x_2,y_2)\)间的“L-距离”定义为\(||P_1P_2||=\left|x_1-x_2\right|+\left|y_1-y_2\right|\)，求平面内与\(x\)轴上两个不同的定点\(F_1,F_2\)的“L-距离”之和等于定值（大于\(||F_1F_2||\)）的点的轨迹形状．
已知三角形\(ABC\)的外接圆圆心为\(O\)，且\(3\overrightarrow {OA}+4\overrightarrow{OB}+5\overrightarrow {OC}=\overrightarrow 0\)，则角\(C\)等于_______．
2011年高考全国卷理科数学第12题（选择压轴题）：
设向量\(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)满足\(\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=1\)，\(\overrightarrow{a}\cdot\overrightarrow{b}=-\dfrac{1}{2}\)，\(\langle\overrightarrow{a}-\overrightarrow{c},\overrightarrow{b}-\overrightarrow{c}\rangle=60^\circ\)，则\(\left|\overrightarrow{c}\right|\)的最大值等于（ ）
A．\(2\)
B．\(\sqrt{3}\)
C．\(\sqrt{2}\)
D．\(1\)
1、（2015年·新课标·文16）已知\(F\)是双曲线\(C:x^2-\dfrac{y^2}{8}=1\)的右焦点，\(P\)是\(C\)的左支上一点，\(A\left(0,6\sqrt 6\right)\)，当\(\triangle APF\)周长最小时，该三角形的面积是_______．
2、（2015年·湖南·理15）已知函数\(f(x)=\begin{cases}x^3,&x\leqslant a\\x^2,&x>a,\end{cases}\)若存在实数\(b\)，使得\(g(x)=f(x)-b\)有两个零点，则\(a\)的取值范围是_______．
3、（2015年·陕西·理16）如图，一横截面为等腰梯形的水渠，因泥沙沉积，导致水渠的界面边界呈抛物线型（图中虚线表示），则原始的最大流量与当前的最大流量的比值为_______．
4、（2014年·湖北·预赛7）在四面体\(ABCD\)中，\(AB=AC=3\)，\(BD=BC=4\)，\(BD\perp ABC\)，则四面体\(ABCD\)的外接球的半径为_______．
5、如图，求四边形\(ABDC\)的面积．
6、（2014年·北京丰台·一模理8）如果某年年份的各位数字之和为\(7\)，，我们称该年为“七巧年”．例如，今年年份\(2014\)的各位数字之和为\(7\)，所以今年恰为“七巧年”．那么从\(2000\)年到\(2999\)年中“七巧年”共有_______个．
7、用\(a\)代表红球，\(b\)代表蓝球，\(c\)代表黑球，由加法原理及乘法原理，从\(1\)个红球和\(1\)个蓝球中取出若干个球的所有取法可由\((1+a)(1+b)\)的展开式\(1+a+b+ab\)表示出来，如：“\(1\)”表示一个球都不取、“\(a\)”表示取出一个红球，而“\(ab\)”则表示把红球和蓝球都取出来.依此类推，下列各式中，其展开式可用来表示从\(5\)个无区别的红球、\(5\)个无区别的蓝球、\(5\)个有区别的黑球中取出若干个球，且所有的蓝球都取出或都不取出的所有取法的是（ ）
A．\(\left(1+a+a^2+a^3+a^4+a^5\right)\left(1+b^5\right)\left(1+c\right)^5\)
B．\(\left(1+a^5\right)\left(1+b+b^2+b^3+b^4+b^5\right)\left(1+c\right)^5\)
C．\(\left(1+a\right)^5\left(1+b+b^2+b^3+b^4+b^5\right)\left(1+c^5\right)\)
D．\(\left(1+a^5\right)\left(1+b\right)^5\left(1+c+c^2+c^3+c^4+c^5\right)\)
已知数列\(\{a_n\}\)满足\(\dfrac{a_{n+1}+a_n-1}{a_{n+1}-a_n+1}=n\)，其中\(n\in \mathcal N^*\)，且\(a_2=6\)，求\(\{a_n\}\)的通项公式．
一、选择题（选对得10分，不选得0分，选错扣5分）
1、整数$x,y,z$满足$xy+yz+zx=1$，则$(1+x^2)(1+y^2)(1+z^2)$可能取到的值为（ ）
A．$16900$
B．$17900$
C．$18900$
D．前三个答案都不对
2015年高考全国卷I 理科数学第5题：
已知\(M(x_0,y_0)\)是双曲线\(C:\dfrac {x^2}{2}-y^2=1\)上的一点，\(F_1\)、\(F_2\)是\(C\)的两个焦点，若\(\overrightarrow {MF_1}\cdot \overrightarrow {MF_2}<0\)，则\(y_0\)的取值范围是（ ）
A．\(\left(-\dfrac {\sqrt {3}}{3},\dfrac {\sqrt {3}}{3}\right)\)
B．\(\left(-\dfrac {\sqrt {3}}{6},\dfrac {\sqrt {3}}{6}\right)\)
C．\(\left(-\dfrac {2\sqrt {2}}{3},\dfrac {2\sqrt {2}}{3}\right)\)
D．\(\left(-\dfrac {2\sqrt {3}}{3},\dfrac {2\sqrt {3}}{3}\right)\)
梅氏定理（梅涅劳斯定理）：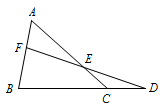 
当直线交\(\triangle ABC\)三边所在直线\(BC,AC,AB\)于点\(D,E ,F\)时，有\(\dfrac {AF}{FB}\cdot \dfrac {BD}{DC}\cdot \dfrac {CE}{EA}=1\)． 塞瓦定理： 
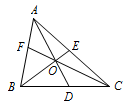在\(\triangle ABC\)内任取一点\(O\)，延长\(AO,BO,CO\)分别交对边于\(D,E,F\)，则\(\dfrac {BD}{DC}\cdot \dfrac {CE}{EA}\cdot \dfrac {AF}{FB}=1\)．
本题要通过梅氏定理与赛瓦定理来解决： \(\triangle ABC\)内有一点\(P\)，连结\(AP,BP,CP\)并延长，分别与对边相交，把\(\triangle ABC\)分成六个小三角形，若这六个小三角形中有三个面积相等，则点\(P\)必为\(\triangle ABC\)的重心．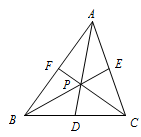 
证明 六个小三角形中有三个面积相等，由对称性可分为四种情况讨论： 情况一 如图①，\(S_{\triangle PBF}=S_{\triangle DPB}=S_ {\triangle PDC}\)； 
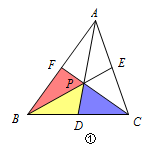此时\(BD=CD\)，所以\(\dfrac{CP}{PF}=2\)， 由梅氏定理可得\(\dfrac{CP}{PF}\cdot \dfrac{AF}{AB}\cdot\dfrac{BD}{DC}=1\)， 所以\(AF=BF\)，即\(P\)为重心． 情况二 如图②，\(S_{\triangle APF}=S_{\triangle DPB}=S_ {\triangle PDC}\)； 
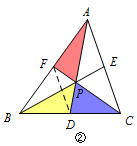可得\(S_{\triangle AFC}=S_{\triangle ADC}\)， 所以\(DF\parallel AC\)， 所以\(D,F\)分别为\(BC,AB\)中点，即\(P\)为重心． 情况三 如图③，\(S_{\triangle FBP}=S_{\triangle DPB}=S_ {\triangle AEP}\)； 
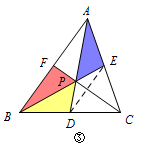此时有\(DE\parallel AB\)， 根据塞瓦定理得\(\dfrac{AF}{BF}\cdot \dfrac{BD}{DC}\cdot \dfrac{CE}{AE}=1\)， 所以\(AF=BF\)，于是\(S_{\triangle APF}=S_{\triangle BPF}\)， 由情况①可得\(P\)为重心． 情况四 如图④，\(S_{\triangle AFP}=S_{\triangle DPB}=S_ {\triangle PCE}\)； 
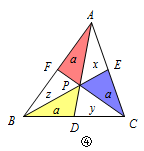根据塞瓦定理得\(\dfrac{S_{\triangle BDP}}{S_{\triangle PDC}}\cdot \dfrac{S_{\triangle PCE}}{S_{\triangle APE}}\cdot \dfrac{S_{\triangle AFP}}{S_{\triangle BFP}}=1\)， 设相等的三角形面积为\(a\)，\(\triangle APE,\triangle CDP\)与\(\triangle BFP\)的面积分别为\(x,y\)与\(z\)，所以\(xyz=a^3\)． ① 若\(x,y,z\)互不相等，不妨设\(x>y>z\)，则\(x>a\)，\(z<a\)，但\[1<\dfrac xa=\dfrac{AE}{CE}=\dfrac{S_{\triangle AEP}}{S_{\triangle CEP}}=\dfrac{S_{\triangle ABP}}{S_{\triangle BCP}}=\dfrac{a+z}{a+y}<1，\]结论矛盾； ② 若\(x,y,z\)中有相等，不妨设\(x=y\)，则\(\dfrac az=\dfrac {a+x}{a+y}=1\)，所以\(a=z\)， 由\(xyz=a^3\)得\(xy=a^2\)，所以\(x=y=z=a\)， 即点\(D,E,F\)分别为各边的中点，\(P\)为重心． 综上，点\(P\)必为\(\triangle ABC\)的重心．
