2014年高考四川卷理科数学第10题(选择压轴题):
已知\(F\)为抛物线\(y^2=x\)的焦点,点\(A\)、\(B\)在该抛物线上且位于\(x\)轴的两侧,\(\overrightarrow{OA}\cdot\overrightarrow{OB}=2\)(其中\(O\)为坐标原点),则三角形\(ABO\)与三角形\(AFO\)的面积之和的最小值是( )
A.\(2\)
B.\(3\)
C.\(\dfrac{17\sqrt 2}8\)
D.\(\sqrt{10}\)
正确答案是 B.
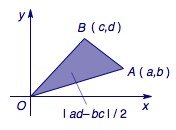
解 首先介绍坐标系下的三角形面积公式,由有向线段\(\overrightarrow{OA}=(a,b)\)和有向线段\(\overrightarrow{OB}=(c,d)\)形成的三角形的有向面积为\[\dfrac 12\begin{vmatrix} a&b\\c&d\end{vmatrix}=\dfrac 12\left(ad-bc\right).\]
证明留给读者(虽然我也很痛恨这句话,但是这个真的很简单).
有了这个公式的知识储备,我们就可以以点构图完成解答.
设\(A\left(a^2,a\right)\)、\(B\left(b^2,b\right)\)、\(F\left(\dfrac 14,0\right)\)且\(a<0<b\).根据对称性,不妨设\(|a|\leqslant |b|\).
由\(\overrightarrow{OA}\cdot\overrightarrow{OB}=2\)可得\[a^2b^2+ab=2,\]从而解得\[\begin{eqnarray}ab=-2,\end{eqnarray}\]进而由坐标系下的三角形面积公式,有\[\begin{split}\triangle ABO+\triangle AFO&=\dfrac 12\left|a^2b-ab^2\right|+\dfrac 12\left|\dfrac 14a\right|\\&=\dfrac 12\left|ab\right|\cdot\left(|a|+|b|\right)+\dfrac 18|a|,\end{split}\]将(1)代入上式,可得所求面积之和为\[\dfrac 98|a|+\dfrac{2}{|a|}\geqslant 2\sqrt{\dfrac 98|a|\cdot\dfrac{2}{|a|}}=3,\]等号当\(|a|=\dfrac 43\)时成立,于是所求面积之和的最小值为\(3\).