在正三角形\(ABC\)的底边\(BC\)上取中点\(M\)，在与底边\(BC\)相邻的两条边\(BA\)和\(CA\)上分别取点\(P\)、\(Q\)，若线段\(PQ\)对\(M\)的张角\(\angle PMQ\)为锐角，则称点\(P\)、\(Q\)亲密．若点\(P\)、\(Q\)在\(BA\)、\(CA\)上的位置随机均匀分布，则\(P\)、\(Q\)亲密的概率称为正三角形的亲密度．试求正三角形的亲密度．
已知\(x,y,z\)均为非负实数，\(x+y+z=3\)，求证：\(x^2y+y^2z+z^2x\leqslant 4\)．
2013年高考江西卷理科数学第10题（选择压轴题，有不影响本质的改动）：
如图，半径为\(1\)的半圆\(O\)与等边三角形\(ABC\)夹在平行线\(l_1\)、\(l_2\)之间，\(l\parallel l_1\)，\(l\)与半圆相交于\(F\)、\(G\)两点，与三角形\(ABC\)两边相交于\(E\)、\(D\)两点．设弧\(FG\)的长为\(x\)（\(0<x<\pi\)），\(y=EB+BC+CD\)，若\(l\)从\(l_1\)平行移动到\(l_2\)，则函数\(y=f(x)\)的图象大致是_______．
数列是定义域离散化的函数，因此我们常常利用数列的通项公式对应的函数研究数列的性质（尤其是数列的单调性）．但在使用这种方法研究数列的单调性时，一定需要时刻提醒自己注意数列的离散特性，否则容易进入以下两种新手常见的误区．
误区一 将函数的单调性等同于数列的单调性
例题1、数列\(\{a_n\}\)的通项公式为\(a_n=2n^2-tn+1,n\in \mathcal N^*\)，若数列\(\{a_n\}\)为递增数列，求实数\(t\)的取值范围．
误解 题意等价为函数\[f(x)=2x^2-tx+1\]在\(x\geqslant 1\)时单调递增，而函数\(f(x)\)的单调递增区间为\(\left[\dfrac t4,+\infty\right)\)，于是由\[\dfrac t4\leqslant 1,\]解得\[t\leqslant 4.\]
正解 当\(n\geqslant 2\land n\in\mathcal N^*\)时，数列\(\{a_n\}\)的阶差\[\begin{split}\Delta a_n&=a_n-a_{n-1}\\&=2n^2-tn+1-\left[2(n-1)^2-t(n-1)+1\right]\\&=4n-(t+2),\end{split}\]于是题意等价为\[\forall n\geqslant 2\land n\in \mathcal N^*,\Delta a_n>0\]于是解得\(t<6\)．
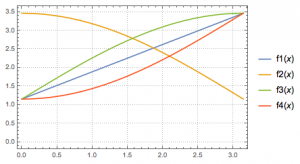
错因 如图，当\(t=5.5\)时，\(f(x)\)虽然不是在\(x\geqslant 1\)上的单调递增函数，但其对应的散点图，也即\(n-a_n\)的图象仍然是上升的．
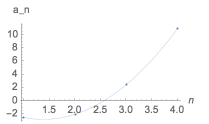
小结 数列的通项公式对应的函数在某区间上存在单调性是数列在对应范围存在单调性的充分非必要条件．
误区二 将函数的最值等同于数列的最值
例题2、数列\(\{a_n\}\)的通项公式\(a_n=\dfrac{n-\sqrt{99}}{n-\sqrt{98}}\)，\(n\in\mathcal N^*\)，请问数列\(\{a_n\}\)是否有最大项和最小项？如果有，请求出；如果没有，请说明理由．
误解 由于数列通项对应的函数\[f(x)=\dfrac{x-\sqrt{99}}{x-\sqrt{98}}\]没有最值，于是数列\(\{a_n\}\)没有最值．
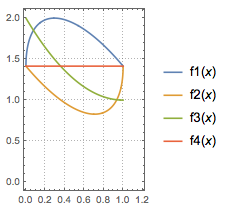
正解 如下图，由数列通项对应的函数\[f(x)=\dfrac{x-\sqrt{99}}{x-\sqrt{98}}\]的图象离散化可以得到数列\(n-a_n\)的图象．
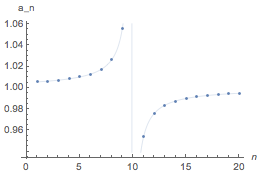
由图象知数列\(\{a_n\}\)中，\(a_9\)为最大项，\(a_{10}\)为最小项．
错因 数列的通项公式对应的函数没有最值并不能保证数列没有最大或最小项．
小结 数列的通项公式对应的函数有最大（小）值是数列有最大（小）项的既不充分也不必要条件．例题给出了不必要的情形，请读者给出不充分的例子．
参考答案 函数\(f(x)=\sin x\)有最大值和最小值，但\(a_n=\sin n,n\in\mathcal N^*\)既没有最大项也没有最小项．
练习 （云南师大附中2015届第7次月考理15文16）已知数列\(\left\{a_n\right\}\)，并且\(a_n=\begin{cases}n^2-5xn+4,&n\leqslant 5,\\(x-23){\log_2}(n-4),&n>5,\end{cases}\)\(n\in\mathcal N^*\)，若\(\{a_n\}\)是递减数列，则实数\(x\)的取值范围是_______．
参考答案 \(\left(\dfrac 95,2\right)\)．
2014年高考天津卷理科数学第14题：
已知函数\(f(x)=\left|x^2+3x\right|\)，\(x\in\mathcal R\)．若方程\(f(x)-a\left|x-1\right|=0\)恰有\(4\)个互异的实数根，则实数\(a\)的取值范围是_______．
2009年北京市中考选择压轴题（2012年定西市中考选择压轴题）：
如图，\(C\)为\(\odot O\)直径\(AB\)上一动点，过点\(C\)的直线交\(\odot O\)于\(D\) 、 \( E \)两点，且\(\angle ACD=45^\circ\)，\(DF\perp AB\) 于点\(F\)，\( EG\perp AB \)于点\( G \)，当点\( C \)在\( AB \)上运动时，设\( AF=x \)，\( DE=y \)，下列图象中，能表示\( y \)与\( x \)的函数关系式的图象大致是_______．
位似旋转变换 设\(O\)为平面上一定点，\(k\)为常数（\(k>0\)），\(\theta\)为有向角，对于任意一点\(P\)，射线\(OP\)绕\(O\)旋转角\(\theta\)，\(P\)映射到\(P'\)，在\(OP'\)射线上存在一点\(P''\)，使\(OP'^\prime =kOP'\)，把由点\(P\)到点\(P'\prime\)的变换叫做以\(O\)为位似旋转中心、旋转角为\(\theta\)、位似比为\(k\)的位似旋转变换，记为\(S\left(O,\theta,k\right)\)．
从位似旋转变换的定义可知，一个位似旋转变换实际是位似变换与旋转变换的复合，此时位似中心与旋转中心重合．位似旋转变换是解决含有特殊系数的线段长度之和的几何极值问题的一种很有效的工具．
2014年高考安徽卷理科数学第10题（选择压轴题）：
在平面直角坐标系\(xOy\)中，已知向量\(\overrightarrow a,\overrightarrow b\)，\(\left|\overrightarrow a\right|=\left|\overrightarrow b\right|=1\)，\(\overrightarrow a\cdot \overrightarrow b=0\)，点\(Q\)满足\(\overrightarrow{OQ}=\sqrt 2\left(\overrightarrow a+\overrightarrow b\right)\)，曲线\(C=\left\{P\left|\overrightarrow{OP}=\cos\theta\overrightarrow a+\sin\theta\overrightarrow b,0\leqslant \theta<2\pi\right.\right\}\)，区域\(\Omega=\left\{P\left|0<r\leqslant \left|\overrightarrow{PQ}\right|\leqslant R,r<R\right.\right\}\)．若\(C\cap \Omega\)为两段分离的曲线，则（ ）
A．\(1<r<R<3\)
B．\(1<r<3\leqslant R\)
C．\(r\leqslant 1<R<3\)
D．\(1<r<3<R\)
