这是我的好朋友凌落蓝提供的一道试题：
已知$f(x)=\dfrac{1+\ln x}{x-1}$，$g(x)=\dfrac kx$（$k\in\mathcal N^*$）．若对任意$c>1$，均存在$a,b$满足$0<a<b<c$，使得$f(c)=f(a)=g(b)$，则$k$的最大值为_______．
仿射变换在解决与椭圆相关的面积问题，特别是面积的最值问题，以及对某些几何的转化中有很好的应用，有时可以大大地简化计算，或将一些题目中隐藏的“平凡”的条件转化成对解题很有利的“特殊”条件． 继续阅读
已知，如图\(BD\perp AC\)，\(\angle AEC=45^\circ\)，\(BD=2CE\)，\(DE\parallel BC\)，求证\(CE=AC+AD\)．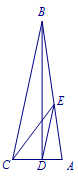
继续阅读
在解析几何中，圆有很多很好的几何性质，比如圆中有垂径定理，可以很好地处理与弦长或者面积相关的问题．椭圆的标准方程\[\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1\]在形式上接近圆的标准方程\[x^2+y^2=r^2,\]我们可以通过仿射变换将椭圆变成圆，再利用圆的良好的几何性质解决问题．我们先来看看什么叫仿射变换？ 继续阅读
已知，如图，在\(\triangle ABC\)中，\(AB=AC\)，延长\(AB\)到\(D\)，延长\(CA\)到\(E\)，连接\(DE\)，使得\(AD=BC=CE=DE\)，求\(\angle BAC\)的度数．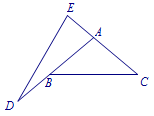
继续阅读
2012年高考山东卷理科数学第12题（选择压轴题）：
设函数$f(x)=\dfrac 1x$，$g(x)=ax^2+bx$（$a,b\in\mathcal R\land a\ne 0$）．若$y=f(x)$的图象与$y=g(x)$的图象有且仅有两个不同的公共点$A(x_1,y_1)$和$B(x_2,y_2)$，则下列判断正确的是（ ）
A．当$a<0$时，$x_1+x_2<0$，$y_1+y_2>0$
B．当$a<0$时，$x_1+x_2>0$，$y_1+y_2<0$
C．当$a>0$时，$x_1+x_2<0$，$y_1+y_2<0$
D．当$a>0$时，$x_1+x_2>0$，$y_1+y_2>0$
【初级】
如图，在\({\rm Rt}\triangle ABC\)中，\(\angle C=90^\circ\)，\(AC:CB=1:3\)，且\(E,D\)是\(BC\)三等分点，求证：\(\angle 1+\angle 2=45^\circ\)．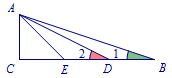
继续阅读
2015年浙江省台州市高三调研试卷理科数学第8题：
在长方体$ABCD-A_1B_1C_1D_1$中，$AB=BC=2$，$AA_1=1$，$E$、$F$为对角线$BD_1$的两个三等分点，$G$为长方体表面上的动点，则$\angle EGF$的最大值为_______．
