该题改编于2010年北京中考第25题（压轴题）：
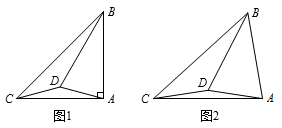
已知\(\triangle ABC\)中，\(\angle BAC=2\angle ACB\)，点\(D\)是\(\triangle ABC\)内的一点，且\(AD=CD\)，\(AB=DB\)．
（1）如图1，当\(\angle BAC=90°\)时，求\(\angle DBC\)与\(\angle ABC\)度数的比值；
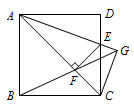
（2）如图2，当\(\triangle ABC\)为锐角三角形时，求\(\angle DBC\)与\(\angle ABC\)度数的比值．
在平面直角坐标系$xOy$中，$O$为坐标原点．定义$P(x_1,y_1)$、$Q(x_2,y_2)$两点之间的“折线距离”为$d(P,Q)=|x_1-x_2|+|y_1-y_2|$．
（1）若点$A(-1,3)$，则$d(A,O)=$_____；
（2）已知点$B(1,0)$，点$M$是直线$l$：$kx-y+k+3=0(k>0)$上的动点，$d(B,M)$的最小值为______；
（3）圆$x^2+y^2=1$上一点与直线$m$：$2x+y-2\sqrt 5=0$上一点的“折线距离”的最小值是______． 继续阅读
如图，在正方形\(ABCD\)中，点\(E\)为\(CD\)上任意一点，\(EF⊥AC\)于点\(F\)，\(BF\)与\(AE\)的延长线交于点\(G\)，连接\(CG\)，则\(\angle BGC=\)____．
$b$克糖水中含有$a$克糖，糖的质量与糖水的质量比为$\dfrac ab$，这个质量比决定了糖水的甜度．如果再添加$m$克糖，生活经验告诉我们糖水会变甜，对应的不等式为$$\dfrac {a+m}{b+m}>\dfrac ab,$$称为糖水不等式，其中$b>a>0,m>0$．这个不等式作差很容易证明，在这里略去．利用糖水不等式可以证明高中的一类形如$$\prod_{i=1}^{n}a_i>f(n)$$的不等式问题．
求证：$\left(1-\dfrac 12\right )\left(1-\dfrac 14\right )\left(1-\dfrac 16\right )\cdots\left(1-\dfrac {1}{2n}\right )<\sqrt{\dfrac {1}{2n+1}}$． 继续阅读
已知平面上两点\(A,B\)，则所有满足\(\dfrac {PA}{PB}=k\)且不等于\(1\)的点\(P\)的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆，又称阿波罗尼斯圆．（当\(k=1\)时，点\(P\)的轨迹为\(AB\)的垂直平分线．）
“渐开数”是指：一个数从第二位起，每一位数字都比其左边数字大的整数（如$236$），那么任取一个三位数，它是“渐开数”的概率为_____．
如图，\(\triangle ABC\)的外心为\(O\)，\(AB=AC\)，\(D\)是\(AB\)的中点，\(E\)是\(\triangle ACD\)的重心．证明：\(OE\perp CD\)．
设等比数列$\{a_n\}$的公比为$q$，其前$n$项的积为$T_n$，并且满足条件$a_1>1$，$a_{99}\cdot a_{100}-1>0$，$\dfrac {a_{99}-1}{a_{100}-1}<0$．给出下列结论，其中正确的结论有______．
① $0<q<1$；
② $a_{99}\cdot a_{101}-1>0$；
③ $T_{100}$的值是$T_n$中最大的；
④ 使$T_n>1$成立的最大自然数$n$等于$198$．
