Math173

已知$a^2+b^2+c^2=2$，求证：$a+b+c\leqslant 2+abc$．

继续阅读 →

函数$f(x)=x|x|$．若存在$x\in[1,+\infty)$，使得$f(x-2k)-k<0$，则$k$的取值范围是(　　)
A．$\left(2,+\infty\right)$
B．$\left(1,+\infty\right)$
C．$\left(\dfrac{1}{2},+\infty\right)$
D．$\left(\dfrac{1}{4},+\infty\right)$

继续阅读 →

已知实数$a_1,a_2,a_3,a_4$满足$a_1a_4-a_2a_3=1$，求$$M=a_1^2+a_2^2+a_3^2+a_4^2+a_1a_3+a_2a_4$$的最小值．

继续阅读 →

已知函数$f(x)={\rm e}^{ax}-x$．
(1) 若曲线$y=f(x)$在$(0,f(0))$处的切线$l$与直线$x+2y+3=0$垂直，求$a$的值；
(2) 当$a\ne 1$时，求证：存在实数$x_0$使$f(x_0)<1$．

继续阅读 →

已知椭圆$G:\dfrac{x^2}{6}+\dfrac{y^2}{b^2}=1$($0<b<\sqrt{6}$)的两个焦点分别为$F_1$和$F_2$，短轴的两个端点分别为$B_1$和$B_2$，点$P$在椭圆$G$上，且满足$\left|PB_1\right|+\left|PB_2\right|=\left|PF_1\right|+\left|PF_2\right|$．当$b$变化时，给出下列三个命题：
(1) 点$P$的轨迹关于$y$轴对称；
(2) 存在$b$使得椭圆$G$上满足条件的点$P$仅有两个；
(3) $|OP|$的最小值为$2$，
其中，所有正确命题的序号是_______．

继续阅读 →

已知两个半径不等的圆盘叠放在一起（有一轴穿过它们的圆心），两圆盘上分别有互相垂直的两条直径将其分为四个区域，小圆盘上所写的实数分别记为$x_1,x_2,x_3,x_4$，大圆盘上所写的实数分别记为$y_1,y_2,y_3,y_4$，如图所示．将小圆盘逆时针旋转$i\ (i=1,2,3,4)$次，每次转动$90^\circ$，记$T_i\ (i=1,2,3,4)$为转动$i$次后各区域内两数乘积之和，例如$T_1=x_1y_2+x_2y_3+x_3y_4+x_4y_1$．若\[x_1+x_2+x_3+x_4<0,\ y_1+y_2+y_3+y_4<0\]则以下结论正确的是(　　)
A．$T_1,T_2,T_3,T_4$中至少有一个为正数
B．$T_1,T_2,T_3,T_4$中至少有一个为负数
C．$T_1,T_2,T_3,T_4$中至多有一个为正数
D．$T_1,T_2,T_3,T_4$中至多有一个为负数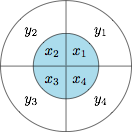 继续阅读 →

有三支股票A、B、C，$28$位股民的持有情况如下：每位股民至少持有其中一支股票．在不持有A股票的人中，持有B股票的人数是持有C股票人数的$2$倍．在持有A股票的人中，只持有A股票的人数比除了持有A股票外，同时还持有其他股票的人数多$1$．在只持有一支股票的人中，有一半持有A股票．则只持有B股票的股民人数是________．

继续阅读 →

已知坐标平面上一点$A(0,6)$，点$B$在$x$轴上运动，$C$是坐标平面内一点且满足$\angle ACB=120^\circ$，$CA=CB$，则线段$OC$长度的最小值是_______．

继续阅读 →