每日一题[247] 从平面到空间

大家应该对这样一道平面轨迹问题不陌生：

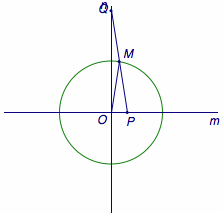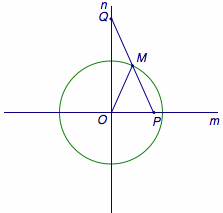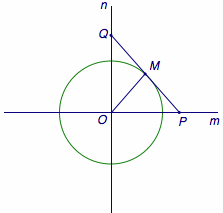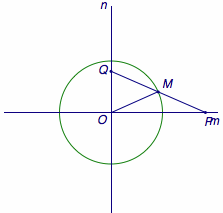
已知\(m\)、\(n\)是互相垂直于点\(O\)的两条直线，长度为\(l\)的线段\(PQ\)的端点\(P\)、\(Q\)分别在直线\(m\)、\(n\)上滑动，求线段\(PQ\)中点的点的轨迹．

由直角三角形斜边上的中线等于斜边的一半，得\(OM=\dfrac 12PQ\)为定值，于是\(M\)的轨迹是以\(O\)为圆心，\(\dfrac 12l\)为半径的圆．

现在思考这个问题的空间版本：

已知\(m\)、\(n\)是异面垂直且距离为\(d\)的两条直线，长度为\(l\)的线段\(PQ\)的端点\(P\)、\(Q\)分别在直线\(m\)、\(n\)上滑动，求线段\(PQ\)中点的点的轨迹．

正确答案是所求轨迹是以\(m\)、\(n\)的公垂线段中点\(O\)为圆心，\(\dfrac 12\sqrt{l^2-d^2}\)为半径的圆，且该圆所在的平面与公垂线段垂直．

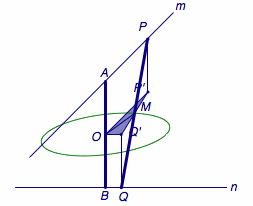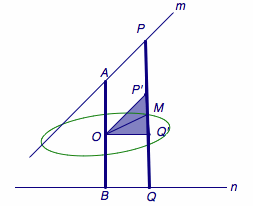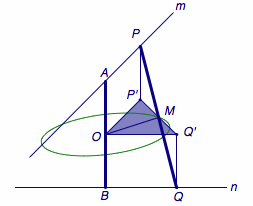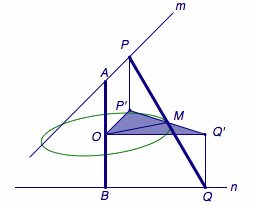
解    如图，设\(m\)、\(n\)的公垂线段为\(AB\)，过线段\(AB\)的中点作\(AB\)的法平面\(\alpha\)，分别作\(P\)、\(Q\)在\(\alpha\)上的投影\(P'\)、\(Q'\)，连接\(OP'\)、\(OQ'\)、\(OM\)、\(P'Q'\)．

由于\(PP'\)与\(QQ'\)平行且相等，于是\(M\)同时平分\(PQ\)与\(P'Q'\)，此时线段\(P'Q'\)仍为定值\(\sqrt{l^2-d^2}\)．

此时问题已经转化为平面上的对应问题，不难得到所求轨迹是以\(m\)、\(n\)的公垂线段中点\(O\)为圆心，\(\dfrac 12\sqrt{l^2-d^2}\)为半径的圆，且该圆所在的平面与公垂线段垂直．

注一    解决立体几何问题的核心思路是通过截割、投影、补形等手段将空间问题转化到平面上，然后利用平面几何知识进行证明及计算．

注二    如果将问题拓展为\(m\)与\(n\)为互相垂直的两个平面，长度固定的线段\(PQ\)的两个端点分别在两个平面上运动 ，那么得到点的轨迹为一个圆柱面及其内部．