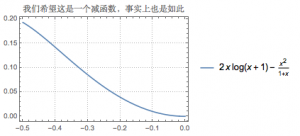
在处理含有参数的导数问题时,通常的作法都是用参数表示所求式子中的零点、极值点、极值等等.但有时直接用参数表示有困难、或者无法用参数表示时,也可能考虑转化变量,但此时一定要注意新设变量的取值范围.
已知函数\(f(x)=x^2+a\ln (x+1)\)有两个相异极值点\(x_1\)、\(x_2\),且\(x_1<x_2\),求证:\(0<\dfrac{f\left(x_2\right)}{x_1}<-\dfrac 12+\ln 2\).
证明 根据已知,函数\(f(x)\)的导函数\[f'(x)=2x+\dfrac{a}{x+1}=\dfrac{1}{x+1}\cdot\left(2x^2+2x+a\right),\]由题意\(f(x)\)有两个极值点,于是\[\begin{cases}\left(2x^2+2x+a\right)_{x=-1}>0,\\\Delta=4-8a>0,\end{cases}\]解得\[0<a<\dfrac 12.\]
由韦达定理,得\[x_1+x_2=-1,x_1x_2=\dfrac a2,\]于是可以将\(\dfrac{f\left(x_2\right)}{x_1}\)化为单一变量的函数.为了避免出现根号,可以选\(x_2\)为变量,即利用代换\[x_1=-1-x_2,a=2\left(-1-x_2\right)x_2,\]得\[\dfrac{f\left(x_2\right)}{x_1}=-\dfrac{x_2^2}{1+x_2}+2x_2\ln\left(x_2+1\right),\]并记右边关于\(x_2\)的函数为\(g\left(x_2\right)\),其中\(x_2=\dfrac{-1+\sqrt{1-2a}}2\),取值范围是\(\left(-\dfrac 12,0\right)\).
不难注意到欲证明不等式即\[g(0)<g\left(x_2\right)<g\left(-\dfrac 12\right),\]因此我们只需要证明\(g\left(x_2\right)\)在\(\left[-\dfrac 12,0\right]\)上单调递减.
事实上,函数\(g\left(x_2\right)\)的导函数\[\begin{split}g'_{x_2}&=2\ln \left(1+x_2\right)+\dfrac{x_2^2}{\left(1+x_2\right)^2}\\&<2x_2+\dfrac{x_2^2}{\left(1+x_2\right)^2}\\&=\dfrac{x_2\left(2x_2+1\right)\left(x_2+2\right)}{\left(1+x_2\right)^2}\\&<0,\end{split}\]于是命题得证.