2001年全俄中学生数学奥林匹克十年级第5题:
已知正数\(a,b,c\)满足\(a+b+c=3\),求证:\(\sqrt a+\sqrt b+\sqrt c\geqslant ab+bc+ca\).
证明 利用恒等式\[(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca,\]可得欲证不等式即\[2\sqrt a+2\sqrt b+2\sqrt c\geqslant 9-a^2-b^2-c^2,\]
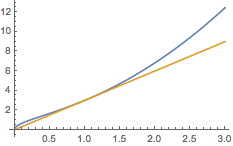
考虑函数\(f(x)=2\sqrt x+x^2\)在\(x=1\)处的切线\(y=3x\),如图.
于是可得局部不等式\[2\sqrt a+a^2\geqslant 3a,\]该不等式也可以对\(\sqrt a+\sqrt a+a^2\)运用算术-几何平均值不等式得到,等号取得的条件为\(a=1\).
因此原不等式得证.
注 在三元均值不等式的证明中,如果能够“分离”变元,就可以考虑利用切线法,可以参考 每日一题[210] 代数不等式的证明 .