每日一题[210] 代数不等式的证明

2015年全国高中数学联赛安徽省预赛第9题：

已知正实数\(a,b\)满足\(a+b=1\)，求证：\(\sqrt{a^2+\dfrac 1a}+\sqrt{b^2+\dfrac 1b}\geqslant 3\)．

法一    均值不等式

注意到取等号的条件为\(a=b=\dfrac 12\)，于是\[\sqrt{a^2+\dfrac 1a}=\sqrt{a^2+\dfrac{1}{8a}+\cdots+\dfrac{1}{8a}}\geqslant 3\sqrt [18]{\dfrac{1}{8^8a^6}},\]类似的，有\[\sqrt{b^2+\dfrac 1b}\geqslant 3\sqrt [18]{\dfrac{1}{8^8b^6}},\]于是\[\begin{split}\sqrt{a^2+\dfrac 1a}+\sqrt{b^2+\dfrac 1b}&\geqslant 3\sqrt [18]{\dfrac{1}{8^8a^6}}+3\sqrt [18]{\dfrac{1}{8^8b^6}}\\&\geqslant 6\sqrt [6]{\dfrac{1}{2^{8}ab}}\\&\geqslant 6\sqrt[6]{\dfrac{4}{2^{8}(a+b)^2}}\\&=3,\end{split}\]因此原不等式得证．

法二    切线法

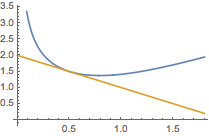
如图，利用切线构造函数不等式\[\sqrt{x^2+\dfrac 1x}\geqslant 2-x,\]应用于\(a\)、\(b\)后两式相加即得．

注    有关切线法的更多题目还可以参考 一个根式函数值域的问题，以及WMTC中的一道试题．

练习    已知\(f(x)=\dfrac{3+x}{1+x^2}\)，\(x\in [0,3]\)，已知数列\(\{a_n\}\)满足\(0<a_n\leqslant 3\)，\(n\in \mathcal N^*\)，且\(a_1+a_2+\cdots+a_{2010}=670\)，则\(f\left(a_1\right)+f\left(a_2\right)+\cdots+f\left(a_{2010}\right)\)的最大值为______．（\(6030\)）

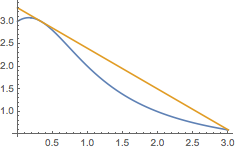
提示    构造\(x\in [0,3]\)上的函数不等式\[\dfrac{3+x}{1+x^2}\leqslant -\dfrac{9}{10}\cdot \left(x-\dfrac 13\right)+3.\]