每日一题[187] 垂径定理与仿射变换

2015年高考浙江卷理科数学第19题（解析几何大题）：

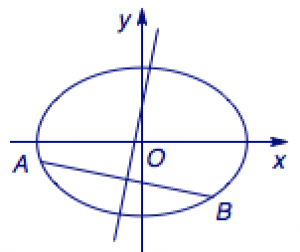
已知椭圆$\dfrac{x^2}{2}+y^2=1$上有两个不同的点$A$、$B$关于直线$y=mx+\dfrac 12$对称．

（1）求实数$m$的取值范围；

（2）求三角形$OAB$面积的最大值（$O$为坐标原点）．

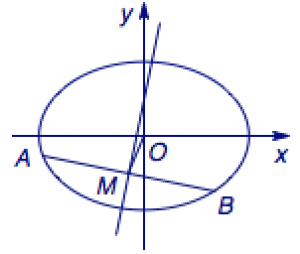
（1）解    如图，设线段$AB$的中点为$M(x_0,y_0)$，则由椭圆的“垂径定理可得 $$\begin{cases}\dfrac{y_0-\frac 12}{x_0}=m,\\-\dfrac 1m\cdot\dfrac{y_0}{x_0}=-\dfrac 12,\end{cases}$$ 解得 $$x_0=-\dfrac 1m,y_0=-\dfrac 12,$$ 结合条件$\dfrac{x_0^2}2+y_0^2<1$可得对$m$的约束 $$\dfrac{1}{2m^2}+\dfrac 14<1,$$ 即 $$m<-\dfrac{\sqrt 6}{3}\lor m>\dfrac{\sqrt 6}{3}.$$

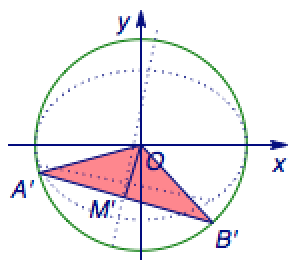
（2）解    如图，作仿射变换 $$\begin{pmatrix}x'\\y'\end{pmatrix}=\begin{pmatrix}1&0\\0&\sqrt 2\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}$$ 将椭圆变成半径为$\sqrt 2$的圆．

此时三角形$OA'B'$的边$A'B'$的中点$M'$在直线$y=-\dfrac{\sqrt 2}2$上运动，于是 $$\begin{split}S_{\triangle OA'B'}&=\dfrac 12\cdot 2\sqrt{2-OM'^2}\cdot OM'\\&=OM'\cdot\sqrt{2-OM'^2}\\&=\sqrt{OM'^2\left(2-OM'^2\right)}\\&\leqslant 1,\end{split}$$ 等号当且仅当$OM'=1$时取得．

于是三角形$OAB$面积的最大值为$\dfrac {\sqrt 2}{2}$．

注    可参考2015年高考数学新课标II卷解析几何大题的解答．