(IMO-56)设\(S\)为平面上一个有限点集,如果对\(S\)中任意两个不同的点\(A\)、\(B\),都存在\(S\)中的一点\(C\),使得\(AC=BC\),我们称\(S\)为平衡的.如果对\(S\)中的任意三个不同点\(A\)、\(B\)、\(C\),都不存在\(S\)中的一点\(P\),满足\(PA=PB=PC\),我们称\(S\)是无中心的.
(1)证明:对每个正整数\(n\geqslant 3\),均存在一个由\(n\)个点构成的平衡的点集;
(2)确定所有的正整数\(n\geqslant 3\),使得存在一个由\(n\)个点构成的平衡且无中心的点集.
(1)证明 从简单情形着手考虑.
当\(n=3\)时,取正三角形\(ABC\)的三个顶点\(A\)、\(B\)、\(C\)即可.
为了得到\(n\)更大的情形,将正三角形\(ABC\)旋转到正三角形\(ADE\),使得\(D\)、\(E\)均不与\(B\)、\(C\)重合.此时\(B\)、\(C\)、\(D\)、\(E\)均在以\(A\)为圆心的圆上,因此它们组成的两点组都由\(A\)进行平衡,而半径\(AB\)与\(AC\)、\(AD\)与\(AE\)均可以构成正三角形,进而构成半径的两点组可以借由与之配对的半径的圆周上的端点进行平衡.这样我们就得到了\(n=5\)的情形.
依次类推,我们可以得到当\(n\)为奇数时的例子.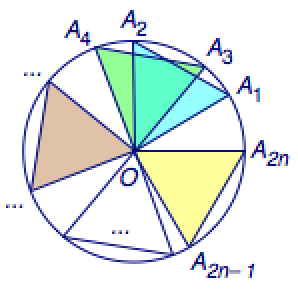
当\(n\)为偶数时,我们只需要将\(n+1\)的例子中使圆周上的某两个点重合即可,如图.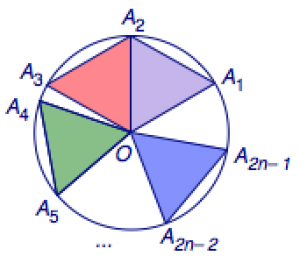
综上,对每个正整数\(n\geqslant 3\),均存在一个由\(n\)个点构成的平衡点集.
(2)解 只有当\(n\)为不小于\(3\)的奇数时,存在由\(n\)个点构成的平衡且无中心的点集,证明如下.
注意到(1)中的例子中,圆心\(O\)为大量三点组的中心,承担着沉重的平衡任务,当要求平衡点集无中心时,很有可能无法完成既定的所有平衡任务,因此考虑平衡任务的数量.
当\(n\)为奇数时,设\(n=2k+1\),\(k\in\mathcal N^*\),此时总平衡任务为\[{\rm C}_n^2=k(2k+1)=2k^2+k,\]而每个点只能平衡其他两两成对的两点组(否则与无中心矛盾),因此最多可以完成平衡任务数为\(k\),于是所有\(2k+1\)个点的最大负载为\[k\cdot (2k+1)=2k^2+k,\]与总的平衡任务数相同.
当\(n\)为偶数时,设\(n=2k+2\),\(k\in\mathcal N^*\),此时总平衡任务数为\[{\rm C}_n^2=(2k+1)(k+1)=2k^2+3k+1,\]而每个点的最大负载为\(k\),于是所有\(2k+2\)个点的最大负载为\[k\cdot (2k+2)=2k^2+2k,\]小于总的平衡任务数.
因此当\(n\)为不小于\(3\)的偶数时,不存在由\(n\)个点构成的平衡且无中心的点集.接下来尝试构造\(n\)为奇数的例子.考虑到此时各个点的负载均衡,因此尝试取正\(n\)边形的\(n\)个顶点.
如图,作正\(n\)边形的外接圆,设\(n=2k+1\),\(k\in\mathcal N^*\).取正\(2k+1\)边形的任意一个顶点,那么正\(n\)边形关于过该顶点的直径所在的直线对称,因此该顶点完成了\(k\)个平衡任务.于是所有的平衡任务均能完成,也就是说,正\(2k+1\)边形的所有顶点构成平衡点集.而很明显,任意三点组的中心均为外接圆圆心,而该圆心并不在平衡点集中,因此该平衡点集是无中心的.
综上,符合题意的所有正整数\(n\)为所有不小于\(3\)的奇数.