2015年高考数学浙江理科第15题（填空压轴题）：
已知\({\vec e_1}\)，\(\vec e_2\)是空间单位向量，\({\vec e_1}\cdot {\vec e_2}=\dfrac 12\)．若空间向量\(\vec b\)满足\({\vec b}\cdot{\vec e_1}=2\)，\({\vec b}\cdot{\vec e_2}=\dfrac 52\)，且对于任意\(x,y\in\mathcal R\)，\(\left|{\vec b}-\left(x{\vec e_1}+y{\vec e_2}\right)\right|\geqslant \left|{\vec b}-\left(x_0{\vec e_1}+y_0{\vec e_2}\right)\right|=1\)（\(x_0,y_0\in\mathcal R\)），则\(x_0=\)_______，\(y_0=\)_______，\(\left|\vec b\right|=\)_______．
正确答案是\(1,2,2\sqrt2\)．
如图，\(\langle \vec e_1,\vec e_2\rangle=\dfrac\pi 3\)．在向量\({\vec e_1}\)，\(\vec e_2\)所在的两条射线上分别取\(OM=2\)，\(ON=\dfrac 52\)，分别过点\(M\)、\(N\)作与射线\(OM\)、\(ON\)垂直的平面，则向量\(\vec b\)的终点\(Q\)在这两个平面的交线上．记此交线与平面\(MON\)的交点为\(P\)．
根据题意，向量\(x\vec e_1+y\vec e_2\)的终点\(R\)可以取遍整个平面\(MON\)，此时\[|QR|=\left|\vec b-\left(x\vec e_1+y\vec e_2\right)\right|,\]其最小值为\(|QP|\)，且\(|QP|=1\)．
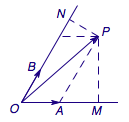
此时分析平面\(MON\)，可以得到\(\overrightarrow{OP}=\vec e_1+2\vec e_2\)，于是\(x_0=1\)，\(y_0=2\)．而\[\left|\vec b\right|^2=|OP|^2+|QP|^2=8,\]因此\(\left|\vec b\right|=2\sqrt 2\)．