每日一题[149] 裂项求和

2015年高考数学广东卷理科第21题（压轴题）：

数列$\left\{a_n\right\}$满足：

$$a_1+2a_2+\cdots+na_n=4-\frac{n+2}{2^{n-1}},n\in\mathcal N^*.$$

（1）求$a_3$的值；

（2）求数列$\left\{a_n\right\}$的前$n$项和$T_n$；

（3）令$b_1=a_1$，$b_n=\dfrac{T_{n-1}}n+\left(1+\dfrac 12+\dfrac 13+\cdots+\dfrac 1n\right)a_n$（$n\geqslant 2$），证明：数列$\left\{b_n\right\}$的前$n$项和$S_n$满足$S_n<2+2\ln n$．

---

（1）解    当$n=1$时，$a_1=1$；

当$n\geqslant 2$时，根据已知可得

$$\begin{split}na_n&=\left(4-\frac{n+2}{2^{n-1}}\right)-\left(4-\frac{n+1}{2^{n-2}}\right)\\&=\frac{n}{2^{n-1}},\end{split}$$ 于是 $$a_n=\frac{1}{2^{n-1}}.$$

综上，$\forall n\in\mathcal N^*,a_n=\dfrac{1}{2^{n-1}}$．

（2）解    $T_n=2-\dfrac{1}{2^{n-1}}$．

（3）证明    不妨记$T_0=0$，这样就有

$$\forall n\in\mathcal N^*,b_n=\dfrac{T_{n-1}}n+\left(1+\dfrac 12+\dfrac 13+\cdots+\dfrac 1n\right)a_n.$$

于是

$$\begin{split}\sum_{k=1}^nb_k&=\sum_{k=1}^n\left[\dfrac{T_{k-1}}{k}+\left(1+\dfrac 12+\cdots+\dfrac 1k\right)a_k\right]\\&=\sum_{k=1}^n\left[\left(1+\dfrac 12+\cdots+\dfrac 1k\right)\cdot\left(T_k-T_{k-1}\right)+\dfrac{T_{k-1}}{k}\right]\\&=\sum_{k=1}^n\left[\left(1+\dfrac 12+\cdots+\dfrac 1k\right)\cdot T_k-\left(1+\dfrac 12+\cdots+\dfrac{1}{k-1}\right)\cdot T_{k-1}\right]\\&=\left(1+\dfrac 12+\cdots+\dfrac 1n\right)\cdot T_n\\&<2\left(1+\dfrac 12+\cdots+\dfrac 1n\right),\end{split}$$ 因此只需要证明 $$\dfrac 12+\dfrac 13+\cdots+\dfrac 1n<\ln n.$$

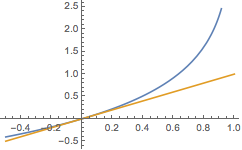
事实上，由于

$$\forall x>0,\ln\dfrac{1}{1-x}>x,$$ 如图（很容易利用导函数证明）．

分别令$x=\dfrac 12,\dfrac 13,\cdots,\dfrac 1n$，累加即得．

---

注一    第（3）小题也可以用阿贝尔求和，

$$\begin{split}\qquad&\sum_{k=1}^{n}\left(1+\dfrac 12+\cdots+\dfrac 1k\right)\cdot\dfrac{1}{2^{k-1}}\\&=1\cdot 1+\left(1+\dfrac 12\right)\cdot \dfrac 12+\left(1+\dfrac 12+\dfrac 13\right)\cdot\dfrac 14+\cdots+\left(1+\dfrac 12+\cdots+\dfrac 1n\right)\cdot\dfrac{1}{2^{n-1}}\\&=1\cdot\left(1+\dfrac 12+\dfrac 14+\cdots+\dfrac{1}{2^{n-1}}\right)+\dfrac 12\left(\dfrac 12+\dfrac 14+\cdots+\dfrac{1}{2^{n-1}}\right)+\cdots+\dfrac 1n\cdot\dfrac{1}{2^{n-1}}\\&=1\cdot T_n+\dfrac 12\cdot \left(T_n-T_1\right)+\cdots+\dfrac{1}{n}\cdot\left(T_n-T_{n-1}\right),\end{split}$$ 于是 $$\begin{split}S_n&=\sum_{k=1}^{n}\dfrac{T_{k-1}}k+\sum_{k=1}^{n}\left(1+\dfrac 12+\cdots+\dfrac 1k\right)\cdot\dfrac{1}{2^{k-1}}\\&=\left(1+\dfrac 12+\cdots+\dfrac 1n\right)\cdot T_n.\end{split}$$

注二    最后一段证明也可以使用数学归纳法或积分放缩法叙述，本质完全相同．